Cho hình bình hành ABCD. Gọi M, N theo thứ tự là trung điểm các cạnh AB, CD. Lấy P thuộc đoạn DM và Q thuộc đoạn BN sao cho DP = 2PM, BQ = xQN.

* Hướng dẫn giải

Lời giải

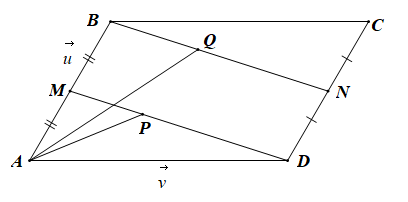
• Vì P thuộc đoạn DM sao cho DP = 2PM

Nên \(\overrightarrow {PD} = - 2\overrightarrow {PM} \)

Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm A ta có:

\(\overrightarrow {AD} - \left( { - 2} \right)\overrightarrow {AM} = \left[ {1 - \left( { - 2} \right)} \right]\overrightarrow {AP} \)

\( \Rightarrow 3\overrightarrow {AP} = \overrightarrow {AD} + 3\overrightarrow {AM} \)

\( \Rightarrow \overrightarrow {AP} = \frac{1}{3}\overrightarrow {AD} + \overrightarrow {AM} \)

\( \Rightarrow \overrightarrow {AP} = \frac{1}{3}\overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} \) (vì M là trung điểm của AB)

\( \Rightarrow \overrightarrow {AP} = \frac{1}{3}\overrightarrow v + \frac{1}{2}\overrightarrow u \)

• Vì Q thuộc đoạn BN sao cho BQ = xQN

\( \Rightarrow \overrightarrow {QB} = - x\overrightarrow {QN} \)

Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm A ta có:

\(\overrightarrow {AB} - \left( { - x} \right)\overrightarrow {AN} = \left[ {1 - \left( { - x} \right)} \right]\overrightarrow {AQ} \)

\( \Rightarrow \left( {1 + x} \right)\overrightarrow {AQ} = \overrightarrow {AB} + x\overrightarrow {AN} \)

\( = \overrightarrow {AB} + x\left( {\overrightarrow {AD} + \overrightarrow {DN} } \right)\)

\( = \overrightarrow {AB} + x\overrightarrow {AD} + x\overrightarrow {DN} \)

\( = \overrightarrow {AB} + x\overrightarrow {AD} + x.\frac{1}{2}\overrightarrow {DC} \) (vì N là trung điểm của CD)

\( = \overrightarrow {AB} + x\overrightarrow {AD} + \frac{1}{2}x\overrightarrow {AB} \) (vì \(\overrightarrow {DC} = \overrightarrow {AB} \))

\( = \left( {1 + \frac{1}{2}x} \right)\overrightarrow {AB} + x\overrightarrow {AD} \)

\( \Rightarrow \left( {1 + x} \right)\overrightarrow {AQ} = \frac{{x + 2}}{2}\overrightarrow u + x\overrightarrow v \)

\( \Rightarrow \overrightarrow {AQ} = \frac{{x + 2}}{{2\left( {x + 1} \right)}}\overrightarrow u + \frac{x}{{x + 1}}\overrightarrow v \) (do x ≠ −1)

b) Với \(\overrightarrow {AP} = \frac{1}{3}\overrightarrow v + \frac{1}{2}\overrightarrow u \) và \(\overrightarrow {AQ} = \frac{{x + 2}}{{2\left( {x + 1} \right)}}\overrightarrow u + \frac{x}{{x + 1}}\overrightarrow v \)

Để A, P, Q thẳng hàng thì hai vectơ \(\overrightarrow {AP} \) và \(\overrightarrow {AQ} \) cùng phương

\( \Leftrightarrow \frac{{\frac{{x + 2}}{{2\left( {x + 1} \right)}}}}{{\frac{1}{3}}} = \frac{{\frac{x}{{x + 1}}}}{{\frac{1}{3}}}\)\( \Leftrightarrow \frac{{x + 2}}{{2\left( {x + 1} \right)}} = \frac{x}{{x + 1}}\)

\( \Leftrightarrow \frac{{x + 2}}{{2\left( {x + 1} \right)}} = \frac{x}{{x + 1}}\)

x + 2 = 2x

x = 2 (thỏa mãn x ≠ –1)

Vậy x = 2 thì ba điểm A, P, Q thẳng hàng.