Cho hình thang vuông ABCD có góc DAB = góc ABC = 90^0 , BC = 1, AB = 2 và AD = 3. Gọi M là trung điểm của AB.Hãy biểu thị các vectơ CM

* Hướng dẫn giải

Lời giải

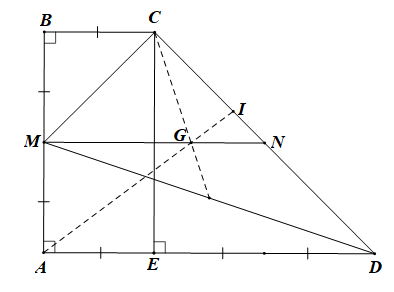
Vì M là trung điểm của AB nên \(\overrightarrow {BM} = \frac{1}{2}\overrightarrow {BA} = - \frac{1}{2}\overrightarrow {AB} \)

Gọi E là hình chiếu của C trên AD. Khi đó \(\widehat {CEA} = 90^\circ \)

Tứ giác ABCE có \[\widehat {DAB} = \widehat {ABC} = \widehat {CEA} = 90^\circ \] nên là hình chữ nhật

EA = CB = 1

Mà AD = 3 do đó AE = \(\frac{1}{3}\)AD

\( \Rightarrow \overrightarrow {EA} = \frac{1}{3}\overrightarrow {DA} = - \frac{1}{3}\overrightarrow {AD} \)

Mà \(\overrightarrow {CB} = \overrightarrow {EA} \) (do ABCE là hình chữ nhật)

\( \Rightarrow \overrightarrow {CB} = - \frac{1}{3}\overrightarrow {AD} \)

\( \Rightarrow \overrightarrow {CM} = \overrightarrow {CB} + \overrightarrow {BM} = - \frac{1}{3}\overrightarrow {AD} - \frac{1}{2}\overrightarrow {AB} \)

• Ta có: \(\overrightarrow {CD} = \overrightarrow {CE} + \overrightarrow {ED} \)

Mà \(\overrightarrow {CE} = \overrightarrow {BA} \) (do ABCE là hình chữ nhật)

Và \(\overrightarrow {ED} = \frac{2}{3}\overrightarrow {AD} \)

\[ \Rightarrow \overrightarrow {CD} = \overrightarrow {BA} + \frac{2}{3}\overrightarrow {AD} = - \overrightarrow {AB} + \frac{2}{3}\overrightarrow {AD} \]

Vậy \(\overrightarrow {CM} = - \frac{1}{3}\overrightarrow {AD} - \frac{1}{2}\overrightarrow {AB} \) và \[\overrightarrow {CD} = - \overrightarrow {AB} + \frac{2}{3}\overrightarrow {AD} .\]