Cho hình thang vuông ABCD có góc DAB = góc ABC = 90^0 , BC = 1, AB = 2 và AD = 3. Gọi M là trung điểm của AB.Gọi N là trung điểm CD, G là trọng tâm tam giác MCD, và I là

* Hướng dẫn giải

Lời giải

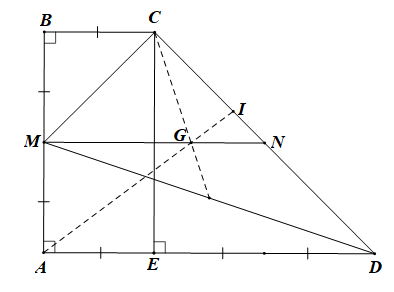
Vì G là trọng tâm của tam giác MCD nên ta có:

\(\overrightarrow {AM} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \)

ABCD là hình chữ nhật nên cũng là hình bình hành

Do đó \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AE} \)

\( \Rightarrow 3\overrightarrow {AG} = \overrightarrow {AM} + \left( {\overrightarrow {AB} + \overrightarrow {AE} } \right) + \overrightarrow {AD} \)

\( = \frac{1}{2}\overrightarrow {AB} + \overrightarrow {AB} + \frac{1}{3}\overrightarrow {AD} + \overrightarrow {AD} \) (do \(\overrightarrow {AE} = \frac{1}{3}\overrightarrow {AD} \))

\( = \frac{3}{2}\overrightarrow {AB} + \frac{4}{3}\overrightarrow {AD} \)

Vì I thuộc cạnh CD nên hai vectơ \(\overrightarrow {IC} \) và \[\overrightarrow {ID} \] ngược hướng nhau

Lại có 9IC = 5ID nên \[9\overrightarrow {IC} = - 5\overrightarrow {ID} \] hay \[\overrightarrow {IC} = - \frac{5}{9}\overrightarrow {ID} \]

Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm A ta có:

\(\overrightarrow {AC} - \left( { - \frac{5}{9}} \right)\overrightarrow {AD} = \left[ {1 - \left( { - \frac{5}{9}} \right)} \right]\overrightarrow {AI} \)

\( \Rightarrow \overrightarrow {AC} + \frac{5}{9}\overrightarrow {AD} = \left[ {1 + \frac{5}{9}} \right]\overrightarrow {AI} \)

\( \Rightarrow \overrightarrow {AC} + \frac{5}{9}\overrightarrow {AD} = \frac{{14}}{9}\overrightarrow {AI} \)

\[ \Rightarrow 14\overrightarrow {AI} = 9\overrightarrow {AC} + 5\overrightarrow {AD} \]

\[ \Rightarrow 14\overrightarrow {AI} = 9\left( {\overrightarrow {AB} + \overrightarrow {AE} } \right) + 5\overrightarrow {AD} \]

\[ \Rightarrow 14\overrightarrow {AI} = 9\overrightarrow {AB} + 9\overrightarrow {AE} + 5\overrightarrow {AD} \]

\[ \Rightarrow 14\overrightarrow {AI} = 9\overrightarrow {AB} + 9.\frac{1}{3}\overrightarrow {AD} + 5\overrightarrow {AD} \]

\[ \Rightarrow 14\overrightarrow {AI} = 9\overrightarrow {AB} + 8\overrightarrow {AD} \]

\[ \Rightarrow 14\overrightarrow {AI} = 6\left( {\frac{3}{2}\overrightarrow {AB} + \frac{4}{3}\overrightarrow {AD} } \right)\]

\[ \Rightarrow 14\overrightarrow {AI} = 6.3\overrightarrow {AG} \] (do \(3\overrightarrow {AG} = \frac{3}{2}\overrightarrow {AB} + \frac{4}{3}\overrightarrow {AD} \))

\[ \Rightarrow 14\overrightarrow {AI} = 18\overrightarrow {AG} \]

\[ \Rightarrow \overrightarrow {AI} = \frac{9}{7}\overrightarrow {AG} \]

Do đó hai vectơ \(\overrightarrow {AI} \) và \[\overrightarrow {AG} \] cùng phương

Suy ra ba điểm A, I, G thẳng hàng.