Cho hình thang vuông ABCD có góc DAB = góc ABC = 90^0, BC = 1, AB = 2 và AD = 3. Gọi M là trung điểm của AB.Tính độ dài các đoạn thẳng AI và BI.

* Hướng dẫn giải

Lời giải

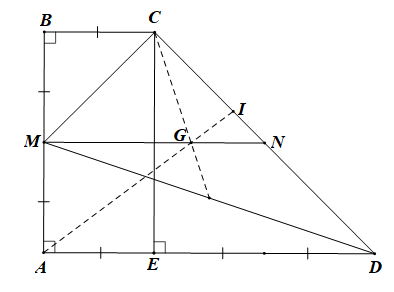
• Theo câu a ta có \[14\overrightarrow {AI} = 9\overrightarrow {AB} + 8\overrightarrow {AD} \]

\[ \Rightarrow {\left( {14\overrightarrow {AI} } \right)^2} = {\left( {9\overrightarrow {AB} + 8\overrightarrow {AD} } \right)^2}\]

\[ \Rightarrow 196A{I^2} = 81A{B^2} + 2.\left( {9\overrightarrow {AB} } \right).\left( {8\overrightarrow {AD} } \right) + 64A{D^2}\]

Mà AB ⊥ AD nên \[\overrightarrow {AB} .\overrightarrow {AD} = 0\]

Do đó ta có: 196AI² = 81AB² + 64AD²

196AI² = 81.2² + 64.3² = 900

AI² = \(\frac{{225}}{{49}}\)

AI = \(\frac{{15}}{7}.\)

• Ta có: \[14\overrightarrow {AI} = 9\overrightarrow {AB} + 8\overrightarrow {AD} \Rightarrow \overrightarrow {AI} = \frac{9}{{14}}\overrightarrow {AB} + \frac{4}{7}\overrightarrow {AD} \]

\(\overrightarrow {BI} = \overrightarrow {AI} - \overrightarrow {AB} = \frac{9}{{14}}\overrightarrow {AB} + \frac{4}{7}\overrightarrow {AD} - \overrightarrow {AB} \)

\( \Rightarrow \overrightarrow {BI} = - \frac{5}{{14}}\overrightarrow {AB} + \frac{4}{7}\overrightarrow {AD} \)

\( \Rightarrow {\left( {\overrightarrow {BI} } \right)^2} = {\left( { - \frac{5}{{14}}\overrightarrow {AB} + \frac{4}{7}\overrightarrow {AD} } \right)^2}\)

\( \Rightarrow B{I^2} = \frac{{25}}{{196}}A{B^2} - 2.\frac{5}{{14}}\overrightarrow {AB} .\frac{4}{7}\overrightarrow {AD} + \frac{{16}}{{49}}A{D^2}\)

\( \Rightarrow B{I^2} = \frac{{25}}{{196}}A{B^2} + \frac{{16}}{{49}}A{D^2}\) (do \[\overrightarrow {AB} .\overrightarrow {AD} = 0\])

\( \Rightarrow B{I^2} = \frac{{25}}{{196}}{.2^2} + \frac{{16}}{{49}}{.3^2} = \frac{{169}}{{49}}\)

BI = \(\frac{{13}}{7}.\)

Vậy AI = \(\frac{{15}}{7}\) và BI = \(\frac{{13}}{7}.\)