Trong mặt phẳng toạ độ Oxy cho ba điểm A(2; −1), B(5; 3) và C(–2; 9). Tìm điểm E thuộc trục hoành sao cho EA + EB nhỏ nhất.

* Hướng dẫn giải

Lời giải

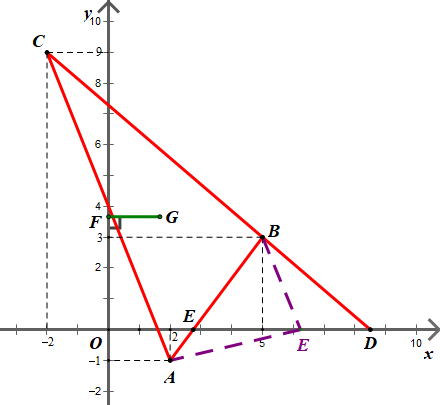
Ta

có: A(2; −1), B(5; 3) là hai điểm nằm về hai phía của trục hoành

Do đó với mỗi điểm E nằm trên trục hoành ta luôn có EA + EB ≥ AB

Suy ra EA + EB ngắn nhất là bằng AB

Điều này xảy ra khi và chỉ khi E là giao điểm của AB và trục hoành Ox

3 điểm A, E, B thẳng hàng

\( \Leftrightarrow \overrightarrow {AB} \) và \(\overrightarrow {AE} \) là hai vectơ cùng phương

Giả sử E(b; 0) là điểm thuộc trục hoành.

Với A(2; −1), B(5; 3) và E(b; 0) ta có:

• \(\overrightarrow {AB} \) = (3; 4)

• \(\overrightarrow {AE} \) = (b – 2; 1)

Khi đó \(\overrightarrow {AB} \) và \(\overrightarrow {AE} \) là hai vectơ cùng phương

\( \Leftrightarrow \frac{{b - 2}}{3} = \frac{1}{4}\)

b – 2 = \(\frac{3}{4}\)

b = \(\frac{{11}}{4}\)

Vậy \(E\left( {\frac{{11}}{4};0} \right)\) là điểm cần tìm.