Tìm điểm M sao cho vecto OM = vecto AB. Từ đó, tìm hoành độ a và tung độ b của vectơ AB

Hướng dẫn giải:

Để xác định điểm M, ta làm như sau:

- Từ đểm O, kẻ đường thẳng d song song với giá của vectơ \(\overrightarrow {AB} \) (chính là đường thẳng AB).

- Lấy điểm M trên đường thẳng d sao cho hai vectơ \(\overrightarrow {AB} ,\,\,\overrightarrow {OM} \) cùng hướng và độ dài đoạn thẳng OM bằng độ dài vectơ \(\overrightarrow {AB} \) (chính là độ dài đoạn thẳng AB).

Ta xác định được điểm M thỏa mãn \(\overrightarrow {OM} = \overrightarrow {AB} \) như hình vẽ:

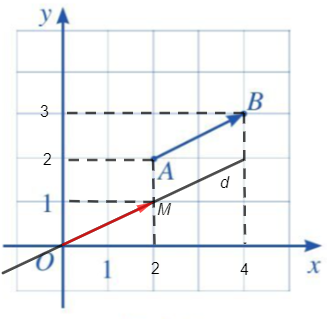
Từ điểm M, kẻ đường thẳng vuông góc với trục hoành, đường thẳng này cắt trục hoành tại điểm ứng với số 2, nên hoành độ của điểm M là x_M = 2.

Từ điểm M, kẻ đường thẳng vuông góc với trục tung, đường thẳng này cắt trục tung tại điểm ứng với số 1, nên tung độ của điểm M là y_M = 1.

Tọa độ của điểm M chính là tọa độ của vectơ \(\overrightarrow {OM} \) nên \(\overrightarrow {OM} = \left( {2;\,\,1} \right)\).

Lại có \(\overrightarrow {OM} = \overrightarrow {AB} \), do đó tọa độ của vectơ \(\overrightarrow {AB} \) là (2; 1).

Vậy hoành độ của vectơ \(\overrightarrow {AB} \) là a = 2 và tung độ của vectơ \(\overrightarrow {AB} \) là b = 1.