Tìm tọa độ điểm M trên đường thẳng BC sao cho diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM.

Hướng dẫn giải:

Vì \(\widehat {ABC} = 127^\circ \) nên tam giác ABC tù.

Kẻ đường cao AH của tam giác ABC, M thuộc đường thẳng BC nên đường cao của tam giác ABM cũng là AH.

Khi đó: S_ABC = \(\frac{1}{2}\)AH . BC và S_ABM = \(\frac{1}{2}\) AH . BM.

Theo bài ra ta có diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM nên S_ABC = 2S_ABM.

Do đó: \(\frac{1}{2}\)AH . BC = 2 . \(\frac{1}{2}\)AH . BM ⇔ BC = 2BM hay BM = \(\frac{1}{2}\)BC.

Suy ra M là trung điểm của BC hoặc M là điểm đối xứng với trung điểm của BC qua B.

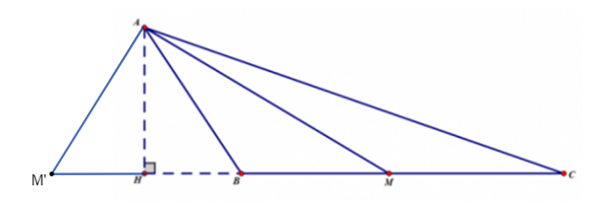
Trường hợp 1: M là trung điểm của BC nên tọa độ của M là \({x_M} = \frac{{{x_B} + {x_C}}}{2} = \frac{{\left( { - 1} \right) + \left( { - 8} \right)}}{2} = \frac{{ - 9}}{2}\), \({y_M} = \frac{{{y_B} + {y_C}}}{2} = \frac{{1 + 2}}{2} = \frac{3}{2}\).

Vậy \(M\left( {\frac{{ - 9}}{2};\,\,\frac{3}{2}} \right)\).

Trường hợp 2: M là điểm đối xứng với trung điểm BC qua B.

Khi đó điểm cần tìm là M', với B là trung điểm của MM'.

Ta có: x_M' = 2x_B – x_M = 2 . (– 1) – \(\frac{{ - 9}}{2} = \frac{5}{2}\), y_M' = 2 . 1 – \(\frac{3}{2} = \frac{1}{2}\).

Vậy \(M'\left( {\frac{5}{2};\,\,\frac{1}{2}} \right)\).