Cho hàm số bậc hai y = ax^2 + bx + c (a ≠ 0) có đồ thị như hình dưới. Khi đó 2a + b + 2c bằng: A. – 9; B. 9; C. – 6; D. 6.
Câu hỏi :
Cho hàm số bậc hai y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới.
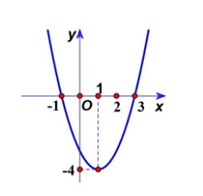
Khi đó 2a + b + 2c bằng:
Cho hàm số bậc hai y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới.

Khi đó 2a + b + 2c bằng:
* Đáp án
* Hướng dẫn giải
Hướng dẫn giải:
Đáp án đúng là: C.
Dựa vào hình vẽ, ta thấy đồ thị hàm số y = ax2 + bx + c có bề lõm hướng lên, đỉnh I(1; –4).
Do đó ta có: a > 0 và a + b + c = – 4 (1)
Đồ thị hàm số còn đi qua các điểm (– 1; 0) và (3; 0).
Khi đó: a – b + c = 0 (2) và 9a + 3b + c = 0 (3).
Lấy (1) trừ vế theo vế cho (2) ta được: 2b = – 4 ⇔ b = – 2.
Thay b = – 2 vào (1) và (3) ta có hệ \(\left\{ \begin{array}{l}a - 2 + c = - 4\\9a + 3.\left( { - 2} \right) + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a + c = - 2\\9a + c = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\c = - 3\end{array} \right.\)
Vậy hàm số y = ax2 + bx + c là y = x2 – 2x – 3.
Khi đó 2a + b + 2c = 2 . 1 + (– 2) + 2 . (– 3) = 2 – 2 – 6 = – 6.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 10 CTST Bài 2. Hàm số bậc hai có đáp án !!
Copyright © 2021 HOCTAP247
