Một chiếc cổng hình parabol có phương trình y = - 1/2x^2. Biết cổng có chiều rộng d = 5 mét. Hãy tính chiều cao h của cổng. A. 4,45 m; B. 3,125 m; C. 4,125 m; D. 3,25 m.

Hướng dẫn giải:

Đáp án đúng là: B.

Gọi A và B là hai điểm ứng với hai chân cổng như hình vẽ.

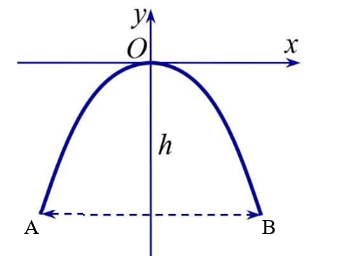
Vì cổng hình parabol có phương trình \(y = - \frac{1}{2}{x^2}\) và cổng có chiều rộng d = 5 m nên:

AB = 5 và hoành độ của A và B lần lượt là \( - \frac{5}{2},\,\,\frac{5}{2}\).

Ta có: \(y = - \frac{1}{2}.{\left( {\frac{5}{2}} \right)^2} = - \frac{1}{2}.{\left( { - \frac{5}{2}} \right)^2} = \frac{{ - 25}}{8}\)

Do đó, \(A\left( {\frac{{ - 5}}{2};\frac{{ - 25}}{8}} \right)\) và \(B\left( {\frac{5}{2};\frac{{ - 25}}{8}} \right)\).

Chiều cao của cổng chính là giá trị tuyệt đối tung độ của A và B hay h = \(\left| {\frac{{ - 25}}{8}} \right| = \frac{{25}}{8} = 3,125\) (m).