Cho tam giác ABC vuông cân tại A có AB = AC = 30 cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC là: A. 50 cm^2; B. 50 căn bậc hai 2 cm^2; C. 75 cm^2; D....

Lời giải

Đáp án đúng là C

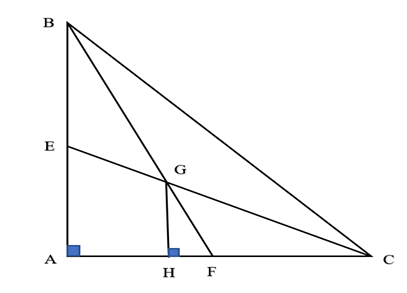
Kẻ GH vuông góc với AC.

G là trọng tâm tam giác ABC ⇒ GF = \(\frac{1}{3}\)BF .

Xét tam giác GFH và tam giác BFA:

\(\widehat {{\rm{GHF}}} = \widehat {{\rm{BAF}}}\)= 90°

\(\widehat {{\rm{GFH}}} = \widehat {{\rm{BFA}}}\)(hay chung \(\widehat {GFH}\))

⇒ tam giác GFH và tam giác BFA đồng dạng (g.g)

⇒ \(\frac{{{\rm{GH}}}}{{{\rm{AB}}}}{\rm{ = }}\frac{{{\rm{GF}}}}{{{\rm{BF}}}}{\rm{ = }}\frac{{\rm{1}}}{{\rm{3}}}\) ( Tính chất hai tam giác đồng dạng)

⇒ GH = 10 cm

Lại có FC = \(\frac{1}{2}\)AC = 15 cm

⇒ S_GFC = 10.15. \(\frac{1}{2}\) = 75 cm²

Vậy đáp án C đúng.