Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Giải SBT Toán 10 Bài tập cuối chương 4 có đáp án !!
Cho góc xOy = 30°. Gọi A và B là...
Cho góc xOy = 30°. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng: A. 1,5; B. căn bậc hai 3; C. 2 căn bậc hai 2; D. 2.
Câu hỏi :
Cho \(\widehat {{\rm{xOy}}}\) = 30°. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:
A. 1,5;
B. \(\sqrt 3 \);
C. \(2\sqrt 2 \);
D. 2.
Cho \(\widehat {{\rm{xOy}}}\) = 30°. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:
A. 1,5;
B. \(\sqrt 3 \);
C. \(2\sqrt 2 \);
D. 2.
* Đáp án
* Hướng dẫn giải
Lời giải
Đáp án đúng là D
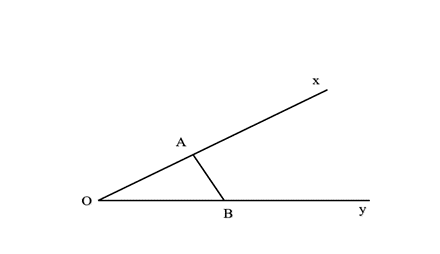
Theo định lí sin ta có:
\[\frac{{{\rm{AB}}}}{{\sin \widehat {\rm{O}}}} = \frac{{{\rm{OB}}}}{{\sin \widehat {\rm{A}}}} = \frac{1}{{\sin 30^\circ }} = 2\]
OB = 2sin\(\widehat {\rm{A}}\).
Ta có –1 ≤ sin\(\widehat {\rm{A}}\)≤ 1 nên OB lớn nhất khi sin\(\widehat {\rm{A}}\) = 1 ⟺ \(\widehat {\rm{A}}\)= 90°.
Khi đó OB = 2.
Đáp án đúng là D.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 10 Bài tập cuối chương 4 có đáp án !!
Số câu hỏi: 60
Copyright © 2021 HOCTAP247
