Hai chiếc tàu thủy P và Q cách nhau 50 m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển, người ta nhìn chiều cao AB của tháp dưới các góc góc BPA= 40° và góc...
Câu hỏi :
Hai chiếc tàu thủy P và Q cách nhau 50 m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển, người ta nhìn chiều cao AB của tháp dưới các góc \(\widehat {{\rm{BPA}}}\)= 40° và \(\widehat {{\rm{BQA}}}\) = 52°. Tính chiều cao của tháp hải đăng đó.
* Đáp án
* Hướng dẫn giải
Lời giải
Ta có hình vẽ sau:
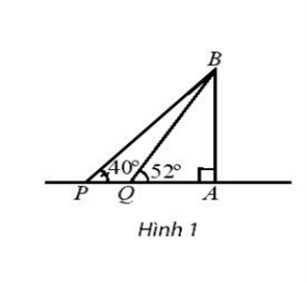
Ta có: \(\widehat {{\rm{BPA}}}\)= 40°, \(\widehat {{\rm{BQA}}}\) = 52°, \(\widehat {{\rm{BAP}}}\)= 90°, PQ = 50 m.
\(\widehat {{\rm{BQP}}}\) là góc kề bù với \(\widehat {{\rm{BQA}}}\) ⇒ \(\widehat {{\rm{BQP}}}\) = 180° – 52° = 128°
Xét tam giác PBQ: \(\widehat {{\rm{PBQ}}}\)+ \(\widehat {{\rm{BQP}}}\)+ \(\widehat {{\rm{BPQ}}}\)= 180°
⇒ \(\widehat {{\rm{PBQ}}}\)= 180° – 128° – 40° = 12°.
Áp dụng định lí sin cho tam giác PBQ ta có:
\(\frac{{{\rm{PQ}}}}{{{\rm{sinB}}}}{\rm{ = }}\frac{{{\rm{BQ}}}}{{{\rm{sinP}}}}\) = \(\frac{{50}}{{\sin 12^\circ }}\) ⇒ BQ = \(\frac{{50}}{{\sin 12^\circ }}\). sinP = \(\frac{{50}}{{\sin 12^\circ }}\).sin40° ≈ 154,58 m.
Xét tam giác ABQ vuông tại A: AB = BQ. sin52° = 154,58. sin52° ≈ 121,81 m.
Vậy chiều cao của tháp hải đăng khoảng 121,81 m.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 10 Bài tập cuối chương 4 có đáp án !!
Copyright © 2021 HOCTAP247
