Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a

* Hướng dẫn giải

Chọn đáp án D

Dựng hình bình hành DBCPnhư hình vẽ.

Từ \(B{\rm{D // CP}} \Rightarrow {\rm{BD // }}\left( {SCP} \right) \Rightarrow d\left( {B{\rm{D}};SC} \right) = d\left( {D;(SCP)} \right) = \frac{1}{2}d\left( {A;(SCP)} \right)\).

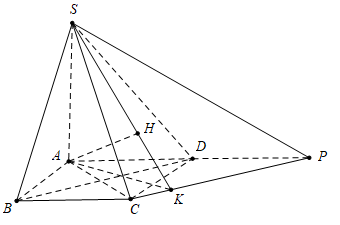Kẻ \(AK \bot CP,{\rm{ }}AH \bot SK \Rightarrow d\left( {A;\left( {SCP} \right)} \right) = AH\)

\( \Rightarrow d\left( {BD;SC} \right) = \frac{1}{2}AH.\)

Ta có \({S_{ACP}} = \frac{1}{2}AK.CP = \frac{1}{2}CD.AP = \frac{1}{2}a.4a = 2{a^2}.\)

Cạnh \(CP = BD = \sqrt {A{B^2} + A{D^2}} = a\sqrt 5 \Rightarrow AK = \frac{{4a}}{{\sqrt 5 }}.\)

\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{K^2}}} = \frac{1}{{4{a^2}}} + \frac{5}{{16{a^2}}} \Rightarrow AH = \frac{{4a}}{3}\)

\( \Rightarrow d\left( {BD;SC} \right) = \frac{1}{2}AH = \frac{{2a}}{3}.\)