Cho tam giác ABC có BC = a, góc BAC = 135 độ. Trên đường thẳng vuông góc với (ABC) tại

* Hướng dẫn giải

Chọn B.

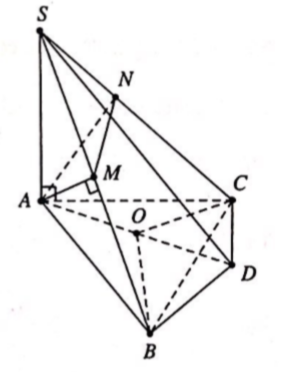
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, và D là điểm đối xứng với A qua O.

Ta có $\mathrm{BD}\perp \mathrm{AB}$ (góc nội tiếp chắn nửa đường tròn).

Và $\mathrm{BD}\perp \mathrm{SA}\Rightarrow \mathrm{BD}\perp \left(\mathrm{SAB}\right)\Rightarrow \mathrm{BD}\perp \mathrm{AM}.$ 

Mặt khác $\mathrm{AM}\perp \mathrm{SB}\Rightarrow \mathrm{AM}\perp \left(\mathrm{SBD}\right)\Rightarrow \mathrm{SD}\perp \mathrm{AM}.$ 

Chứng minh tương tự ta được $\mathrm{SD}\perp \mathrm{AN}\Rightarrow \mathrm{SD}\perp \left(\mathrm{AMN}\right).$ 

Ta có $\left\{\begin{array}{l}\mathrm{SD}\perp \left(\mathrm{AMN}\right)\\ \mathrm{SA}\perp \left(\mathrm{ABC}\right)\end{array}\right.\Rightarrow \left(\widehat{\left(\mathrm{AMN}\right);\left(\mathrm{ABC}\right)}\right)$

$=\left(\widehat{\mathrm{SA};\mathrm{SD}}\right)=\widehat{\mathrm{ASD}}.$ 

Ta có: AD$=2{\mathrm{R}}_{\mathrm{ABC}}=\frac{\mathrm{BC}}{\sin \hat{\mathrm{A}}}=\mathrm{a}\sqrt{2}$

Vậy $\left(\widehat{\left(\mathrm{AMN}\right);\left(\mathrm{ABC}\right)}\right)=\widehat{\mathrm{ASD}}=\arctan 1={45}^{\mathrm{o}}$