Trang chủ
Đề thi & kiểm tra
Toán học
Tổng hợp đề thi thử thpt quốc gia môn Toán cực hay mới nhất !!
Cho khối trụ có hai đáy là hình tròn (O;R)...
Cho khối trụ có hai đáy là hình tròn (O;R) và (O';R), OO' = 4R
Câu hỏi :
Cho khối trụ có hai đáy là hình tròn (O;R) và . Trên đường tròn tâm O lấy (O) lấy hai điểm A, B sao cho . Mặt phẳng (P) đi qua A, B cắt OO’ và tạo với đáy một góc bằng . (P) cắt khối trụ theo thiết diện là một phần của elip. Diện tích thiết diện đó bằng:
A.
B.
C.
D.
* Đáp án
C
* Hướng dẫn giải
Đáp án C
Phương pháp:
+) Chứng minh mặt phẳng (P) không cắt đáy (O';R)
+) Tìm phần hình chiếu của mặt phẳng (P) trên mặt đáy. Tính
+) Sử dụng công thức
Cách giải:
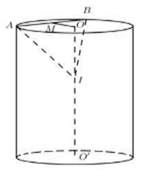
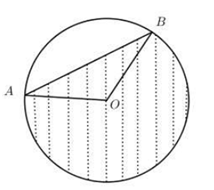
Gọi M là trung điểm của AB ta có:
Giả sử mặt phẳng (P) cắt trục OO’ tại I. Ta có : IA = IB nên cân tại I, do đó

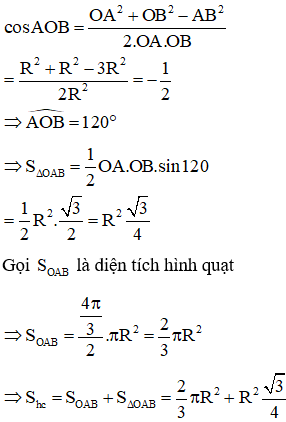
Vậy diện tích phần thiết diện cần tìm là :
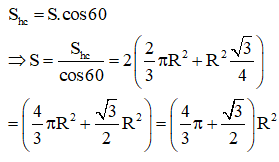
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Tổng hợp đề thi thử thpt quốc gia môn Toán cực hay mới nhất !!
Số câu hỏi: 498
Copyright © 2021 HOCTAP247
