Cho hàm số y = x^3 - 3x + 2 có đồ thị (C). Hỏi có bao nhiêu

* Hướng dẫn giải

Đáp án C

Phương pháp:

Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ 

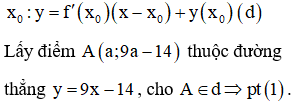
Để  từ  A  kẻ  được  hai  tiếp  tuyến đến (C) thì phương trình (1) có 2 nghiệm  phân  biệt. Tìm điều  kiện  của a để phương trình có 2 nghiệm  phân  biệt.  Có  bao  nhiêu  giá  trị  của  a  thì  có  bấy nhiêu điểm  thỏa  mãn  yêu  cầu  bài toán.

Cách giải:

TXĐ : D = R.

$9a-14=\left(3x_0^2-3\right)\left(a-x_0\right)+x_0^3-3x_0+2\left(1\right)$

$\iff 9a-14=3a{x}_0^2-3x_0^3-3a+3x_0+x_0^3-3x_0+2$

$\iff -2x_0^3+3a{x}_0^2-12a+16=0$

$\iff \left(x_0-2\right)\left(-2x_0^2+\left(3a-4\right)x_0+6a-8\right)=0$

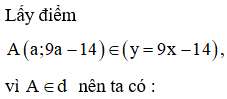
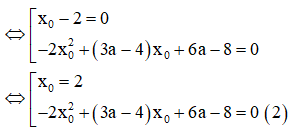
Để qua A kẻ được 2 tiếp tuyến đến đồ thị (C) thì phương trình (1) có 2 nghiệm phân biệt.

TH1 : $x_0=2$  là nghiệm của phương trình (2) ta có : 

TH2 : $x_0=2$ không là nghiệm của phương trình (2), khi đó để (1) có 2 nghiệm phân biệt thì (2) có nghiệm kép khác 2.

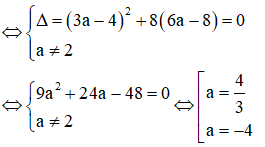
Vậy có 3 giá trị của a thỏa mãn yêu cầu bài toán.

Chú ý và sai lầm: Cần phải làm hết các trường hợp để phương trình (1) có 2 nghiệm, tránh trường hợp thiếu TH1 và chọn nhầm đáp án B.