75 câu trắc nghiệm Vectơ nâng cao !!
Câu 1 : Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 2 : Cộng các vectơ có cùng độ dài 5 và cùng giá. Khẳng định nào sau đây đúng?
A. Cộng 5 vectơ ta được kết quả là
B. Cộng 6 vectơ đôi một ngược hướng ta được kết quả là
C. Cộng 121 vectơ ta được kết quả là
D. Cộng 25 vectơ ta được vectơ có độ dài là 0.
Câu 3 : Cho tứ giác ABCD. Điều kiện cần và đủ để ?
A. ABCD là hình bình hành
B. ABDC là hình bình hành.
C. AD và BC có cùng trung điểm
D. AB= CD
Câu 4 : Cho tứ giác ABCD. Gọi M; N; P; Q lần lượt là trung điểm của AB; BC; CD ; DA. Khẳng định nào sai.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 5 : Cho tam giác ABC vuông cân đỉnh A, đường cao AH. Khẳng định nào sau đây sai?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 6 : Cho hình thoi ABCD cạnh a và góc . Đẳng thức nào sau đây đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 7 : Cho 2 điểm phân biệt A; B và 1 điểm C. Có bao nhiêu điểm D thỏa mãn
A. 0
B. 1
C. 10
D. vô số
Câu 8 : Cho tam giác ABC có M thỏa mãn điều kiện . Xác định vị trí điểm M
A. M là điểm thứ tư của hình bình hành ACBM
B.M là trung điểm của đoạn thẳng AB
C.M trùng C
D.M là trọng tâm tam giác ABC
Câu 9 : Cho tam giác ABC. Tập hợp các điểm thỏa mãn là?
A. đường thẳng AB
B. trung trực đoạn BC
C. đường tròn tâm A: bán kính BC
D. đường thẳng qua A và song song với BC
Câu 10 : Cho hình bình hành ABCD. Tập hợp các điểm M thỏa mãn là?
A. một đường tròn.
B. một đường thẳng.
C. tập rỗng.
D. một đoạn thẳng.
Câu 11 : Gọi O là tâm của hình vuông ABCD. Vectơ nào trong các vectơ dưới đây bằng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 12 : Cho tam giác ABC và điểm M thỏa mãn . Tìm vị trí điểm M.
A. M là trung điểm của AC
B.M là trung điểm của AB
C.M là trung điểm của BC
D.M là điểm thứ tư của hình bình hành ABCM
Câu 13 : Cho tam giác ABC. Hai điểm M, N được xác định bởi hệ thức:
A. MN và AC song song
B. MN và AC cắt nhau
C. MN= AC
D. 3 điểm M; A; C thẳng hàng
Câu 14 : Cho tứ giác ABCD. Gọi I ; K lần lượt là trung điểm của AB; CD. Xác định vị trí điểm G sao cho:
A. G là trung điểm của BI
B. G là trung điểm của KD
C. G là trung điểm của BD
D. G là trung điểm của IK
Câu 15 : Cho tam giác ABC. Tìm điểm M thỏa mãn
A. M là trung điểm cạnh IC , với I là trung điểm của cạnh AB
B. M trùng với đỉnh C của tam giác ABC
C. M là trọng tâm của tam giác ABC.
D. M là đỉnh của hình bình hành MCAB
Câu 16 : Cho hai tam giác ABC và A'B'C' lần lượt có trọng tâm là G và G'. Đẳng thức nào sau đây là sai?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 17 : Cho hình bình hành ABCD, điểm M thoả mãn: . Khi đó M là trung điểm của:
A.AB
B.BC
C. AD
D. CD
Câu 18 : Gọi M; N lần lượt là trung điểm của các cạnh AB và CD của tứ giác ABCD. Mệnh đề nào sau đây đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 19 : Gọi O là tâm hình bình hành ABCD; hai điểm E; F lần lượt là trung điểm AB; BC. Đẳng thức nào sau đây sai?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 20 : Cho hình bình hành ABCD. Gọi G là trọng tâm của tam giác ABC. Mệnh đề nào sau đây đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 21 : Tam giác ABC có AB= AC= a ; . Tính độ dài vectơ tổng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 22 : Cho tam giác ABC đều cạnh a, H là trung điểm của BC. Tính
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 23 : Gọi M; N lần lượt là trung điểm các cạnh AD; BC của tứ giác ABCD. Đẳng thức nào sau đây sai?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 24 : Cho tam giác ABC có trung tuyến AM, gọi I là trung điểm AM. Đẳng thức nào sau đây đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 25 : Gọi AN; CM là các trung tuyến của tam giác ABC. Đẳng thức nào sau đây đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 26 : Cho tam giác ABC với phân giác trong AD. Biết AB= 5; BC= 6; CA= 7. Khi đó bằng
A. 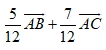
B. 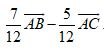
C. 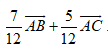
D. ![]()
Câu 27 : Cho AD và BE là hai phân giác trong của tam giác ABC. Biết AB= 4, BC= 5 và CA= 6. Khi đó bằng:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 28 : Cho tam giác ABC có I; D lần lượt là trung điểm AB; CI điểm N thuộc cạnh BC sao cho BN= 2NC. Đẳng thức nào sau đây đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 29 : Cho hình vuông ABCD có độ dài cạnh 3. Giá trị của là bao nhiêu?
A. 6.
B.
C. 12
D. 0
Câu 30 : Cho hình thoi ABCD có AC= 2a; BD= a. Tính
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 31 : Cho tam giác ABC, tập hợp các điểm M sao cho là:
A. một đường thẳng đi qua trọng tâm của tam giác.
B. đường tròn có tâm là trọng tâm của tam giác và bán kính bằng 6.
C. đường tròn có tâm là trọng tâm của tam giác và bán kính bằng 2.
D. đường tròn có tâm là trọng tâm của tam giác và bán kính bằng 18
Câu 32 : Cho tam giác đều ABC cạnh bằng 1. Tính
A.
B. 1
C. 2
D. 3
Câu 33 : Cho tam giác ABC đều cạnh 2a. Khi đó độ dài vectơ bằng
A. 2a
B.
C. 4a
D.
Câu 34 : Cho hình thoi ABCD có cạnh bằng a, . Tính
A.
B. 2a
C.
D. a
Câu 35 : Cho tam giác ABC vuông cân tại C; . Tính
A.
B. 5
C. 1
D.
Câu 36 : Cho hình thang ABCD có AB song song với CD. Cho AB=2a và CD= a. Gọi O là trung điểm của AD. Khi đó:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 37 : Cho hình vuông ABCD cạnh . Tính ?
A. 2a
B. a
C.
D.
Câu 38 : Cho hình thang ABCD có AB song song với CD. Cho AB= 2a,CD= a. Gọi O là trung điểm của AD. Khi đó
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 39 : Cho tam giác ABC vuông cân tại A có , M là trung điểm của BC. Khẳng định nào sau đây đúng
A. ![]()
B. ![]()
C. ![]()
D. Tất cả sai
Câu 40 : Tam giác ABC vuông tại A; AB= AC= 2. Độ dài vectơ bằng:
A.
B. 5
C. 12
D.
Câu 41 : Cho đoạn thẳng AB có độ dài bằng a. Một điểm M di động sao cho . Gọi H là hình chiếu của M lên AB. Tính độ dài lớn nhất của MH?
A.
B.
C. a
D. 2a
Câu 42 : Cho hai điểm cố định A; B. gọi I là trung điểm của AB. Tập hợp các điểm M thoả: là:
A. Đường tròn đường kính AB.
B. Trung trực của AB.
C. Đường tròn tâm I, bán kính AB.
D. Nửa đường tròn đường kính AB
Câu 43 : Cho tam giác ABC, có bao nhiêu điểm M thỏa ?
A. 1
B. 2
C. vô số.
D. Không có điểm nào.
Câu 44 : Cho tam giác ABC. Tập hợp các điểm M thỏa mãn là?
A. đường thẳng AB
B. trung trực đoạn BC
C. đường tròn tâm A; bán kính BC
D. đường thẳng qua A và song song với BC
Câu 45 : Cho hình bình hành ABCD. Tập hợp các điểm M thỏa mãn là?
A. một đường tròn
B. một đường thẳng.
C. tập rỗng.
D. một đoạn thẳng
Câu 46 : Cho tam giác ABC và điểm M thỏa mãn . Tìm vị trí điểm M
A. M là trung điểm của AC
B.M là trung điểm của AB
C.M là trung điểm của BC
D.M là điểm thứ tư của hình bình hành ABCM
Câu 47 : Cho tam giác ABC và điểm M thỏa mãn điều kiện . Mệnh đề nào sau đây sai?
A. MABC là hình bình hành.
B. ![]()
C. ![]()
D. ![]()
Câu 48 : Cho I; J; K lần lượt là trung điểm của các cạnh AB; BC; CA của tam giác ABC. Giả sử M là điểm thỏa mãn điều kiện . Khi đó vị trí điểm M là:
A. M là giao điểm 2 đường chéo của hình bình hành BIKJ.
B.M là đỉnh thứ tư của hình bình hành AIKM.
C. M là trực tâm của tam giác ABC.
D.M là trọng tâm của tam giác IJK.
Câu 49 : Trên trục cho 3 điểm A; B; C có tọa độ lần lượt là a; b;c . Tìm điểm I sao cho
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 50 : Trên trục , cho ba điểm A; B; C lần lượt có tọa độ là -5; 2; 4. Tìm tọa độ điểm M thỏa mãn
A. 10/3
B. -10/3
C. 10/9
D. 9/10
Câu 51 : Trong mặt phẳng tọa độ Oxy. Cho hình thoi ABCD cạnh a và . Biết A trùng với gốc tọa độ O; C thuộc trục Ox và xB; yB ≥ 0. Tìm tọa độ các đỉnh B và C của hình thoi ABCD.
A. 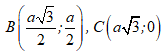
B. 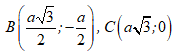
C. 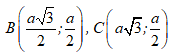
D. 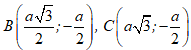
Câu 52 : Trong mặt phẳng Oxy, cho các điểm A(-3; 3) ; B(1; 4) ; C( 2; -5). Tọa độ điểm M thỏa mãn là:
A. 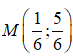
B. ![]()
C. 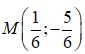
D. 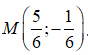
Câu 53 : Cho M(2 ; 0) : N( 2 ; 2) và P( -1 ; 3) lần lượt là trung điểm các cạnh BC ; CA ; AB của tam giác ABC. Tọa độ B là:
A.(1;1)
B.(-1;-1)
C.(-1;1)
D. (1;-1)
Câu 54 : Trong mặt phẳng tọa độ , cho tam giác MNP có M(1;-1) : N(5; -3) và P thuộc trục Oy, trọng tâm G của tam giác nằm trên trục Ox.Toạ độ của điểm P là
A.(0;4)
B.(4;0)
C.(2;4)
D.(2;0)
Câu 55 : Cho tam giác ABC với AB= 5 và AC=1. Tính toạ độ điểm D là của chân đường phân giác trong góc A, biết B(7; -2) và C(1;4)
A. 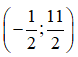
B.(2;3)
C.(0;2)
D.(1;1)
Câu 57 : Trong hệ trục tọa độ Oxy, cho hình vuông ABCD tâm O và có A(1;3) . Biết điểm B thuộc trục Ox và cùng hướng với . Tìm tọa độ các vectơ ?
A.(1;2)
B.(3;4)
C.(3;-3)
D.(3;0)
Câu 58 : Trong mặt phẳng Oxy, cho A(m-1; -1) ; B(2; 2-2m) ; C(m+3; 3). Tìm giá trị m để A; B; C là ba điểm thẳng hàng?
A. m= 2
B. m=0
C. m=1
D. m=-2
Câu 59 : Trong mặt phẳng tọa độ oxy cho 4 điểm A(0;1) ; B(1;3) ; C(2;7) và D(0;3). Tìm giao điểm của 2 đường thẳng AC và BD.
A.
B.
C.
D.
Câu 60 : Trong mặt phẳng tọa độ Oxy, cho ba điểm A(6,3) ; B(-3;6) và C(1; -2). Xác định điểm E trên cạnh BC sao cho BE= 2EC.
A.
B.
C.
D.
Câu 61 : Trong mặt phẳng tọa độ Oxy, cho 4 điểm A(6;3) ; B( -1/3; 2/3); C(1; -2) và D( 15;0). Xác định giao điểm I hai đường thẳng BD và AC.
A. (3 ;2)
B. (3 ; 7)
C.
D.(6 ; 1)
Câu 62 : Cho ba điểm A(-1; -1) ; B( 0;1) ; C(3;0). Xác định tọa độ điểm D biết D thuộc đoạn thẳng BC và 2BD= 5DC.
A. 
B. ![]()
C. 
D. 
Câu 63 : Cho hình bình hành ABCD có A(-2; 3) và tâm I(1;1) . Biết điểm K(-1;2) nằm trên đường thẳng AB và điểm D có hoành độ gấp đôi tung độ. Tìm tổng hoành độ của B và D
A.1
B.3
C.2
D.4
Câu 64 : Cho tam giác ABC có A( 3;4) : B( 2;1) và C( -1; -2). Tìm điểm M trên đường thẳng BC sao cho SABC= 3SAMB.
A. M(0 ;1)
B.M( 1;0)
C. M (3 ;2)
D. cả C và B đúng
Câu 65 : Trong mặt phẳng tọa độ Oxy cho . Cho biết . Khi đó
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 66 : Cho các vectơ . Phân tích vectơ theo hai vectơ và , ta được:
A.
B.
C.
D.
Câu 67 : Cho hai điểm M(8; -1) và N( 3;2). Nếu P là điểm đối xứng với điểm M qua điểm N thì P có tọa độ là:
A.(-2;5)
B.(2; -3)
C.(4; -1)
D.(4; -6)
Câu 68 : Cho hình vuông ABCD cạnh a. Hỏi mệnh đề nào sau đây đúng
A. ![]() không phụ thuộc vào vị trí điểm M.
không phụ thuộc vào vị trí điểm M.
B. Độ dài vectơ u là 2.
C. Cả A và B sai.
D .cà A và B đúng
Câu 69 : Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ Mệnh đề nào sau đây đúng?
A.
B.
C.
D. Tất cả sai
Câu 70 : Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ . Tính vecto tổng
A. vecto AD
B. Vecto BC
C. Vecto DI
D. Vecto 0
Câu 71 : Cho tam giác ABC có tâm đường tròn ngoại tiếp O, H là trực tâm. Tính
A.
B.
C.
D. Tất cả sai
Câu 72 : Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O. Tính
A.
B.
C.
D. Tất cả sai
Câu 73 : Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC; CA: AB.Tìm mệnh đề đúng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Câu 74 : Cho tứ giác ABCD. Gọi I là trung điểm BC. Xác định điểm M sao cho
A. M là trung điểm BI
B. M là trung điểm AC
C. M là trung điểm AB
D. M là trung điểm AI
Câu 75 : Cho tứ giác ABCD. Gọi I là trung điểm BC. Xác định điểm M sao cho
A. P là trung điểm BG
B. P là trung điểm AG
C. P là trung điểm CG
D. P là trọng tâm tam giác
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247