Cho hình chóp S.ABCD có SA = 2a, SB = 3a, SC = 4a và

Chọn B.

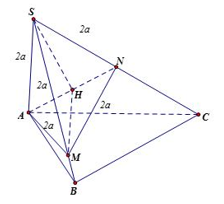
Lấy điểm M, N lần lượt thuộc cạnh SB, SC sao cho SM = SN = 2a. Suy ra tam giác SAM, SMN đều cạnh có độ dài 2a tam giác SAN vuông cân tại S và $AN=2a\sqrt{2}.$

Trong tam giác AMN có $A{M}^2+M{N}^2=A{N}^2$ và AM = MN nên tam giác AMN vuông cân tại M

Từ S hạ $SH\perp AN$ tại H suy ra H là trung điểm $AN,MH=a\sqrt{2}$ và $SH=a\sqrt{2}.$

Trong tam giác SHM ta có $M{H}^2+S{H}^2={\left(a\sqrt{2}\right)}^2+{\left(a\sqrt{2}\right)}^2=4a^2=S{M}^2$ nên tam giác SHM vuông tại H. Suy ra có $\left.\begin{array}{l}SH\perp AM\\ SH\perp HM\end{array}\right\}\Rightarrow SH\perp \left(AMN\right)$ tại H

$V_{SAMN}=\frac{1}{3}{S}_{AMN}.SH=\frac{1}{3}.\frac{1}{2}.2a.2a.a\sqrt{2}=\frac{2a^3\sqrt{2}}{3}.$

$\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SM}{SB}.\frac{SN}{SC}=\frac{2}{3}.\frac{1}{2}=\frac{1}{3}\Rightarrow V_{S.ABC}=3V_{S.AMN}=3\frac{2a^3\sqrt{2}}{3}=2a^3\sqrt{2}.$