Có bao nhiêu số nguyên m để hàm số f(x) = 3x +m căn bậc hai của x^2 + 1

Phương pháp:

- Tính đạo hàm f'(x)

- Để hàm số $f\left(x\right)=3x+m\sqrt{x^2+1}$ đồng biến trên $ℝ$ thì $f\text{'}\left(x\right)\ge 0\forall x\in ℝ$ và bằng 0 tại hữu hạn điểm.

- Chia TH của x cô lập m.

- Giải các bất phương trình: $\left\{\begin{array}{l}m\ge f\left(x\right)\forall x\in \left[a;b\right]\Rightarrow m\ge \underset{\left[a;b\right]}{\max }f\left(x\right)\\ m\le f\left(x\right)\forall x\in \left[a;b\right]\Rightarrow m\le \underset{\left[a;b\right]}{\min }f\left(x\right)\end{array}\right.$

Cách giải:

TXĐ: $D=ℝ$

Ta có $f\left(x\right)=3x+m\sqrt{x^2+1}\Rightarrow f\text{'}\left(x\right)=3+\frac{mx}{\sqrt{x^2+1}}.$

Để hàm số $f\left(x\right)=3x+m\sqrt{x^2+1}$ đồng biến trên $ℝ$ thì $f\text{'}\left(x\right)\ge 0\forall x\in ℝ$ và bằng 0 tại hữu hạn điểm.

$\iff 3+\frac{mx}{\sqrt{x^2+1}}\ge 0\forall x\in ℝ\iff \frac{3\sqrt{x^2+1}+mx}{\sqrt{x^2+1}}\ge 0\forall x\in ℝ$

$\iff 3\sqrt{x^2+1}+mx\ge 0\forall x\in ℝ\iff mx\ge -3\sqrt{x^2+1}\forall x\in ℝ$

TH1: $x=0\Rightarrow 0\ge -3$ (luôn đúng).

TH2: $x>0\Rightarrow m\ge \frac{-3\sqrt{x^2+1}}{x}=f\left(x\right)\Rightarrow m\ge \underset{\left(0;+\infty \right)}{\max }f\left(x\right)\left(1\right).$

TH3: $x<0\Rightarrow m\le \frac{-3\sqrt{x^2+1}}{x}=f\left(x\right)\Rightarrow m\le \underset{\left(0;+\infty \right)}{\min }f\left(x\right)\left(2\right).$

Xét hàm số $f\left(x\right)=-\frac{3\sqrt{x^2+1}}{x}\left(x\ne 0\right)$ ta có $f\text{'}\left(x\right)=\frac{\frac{-3x}{\sqrt{x^2+1}}x+3\sqrt{x^2+1}}{x^2}=\frac{3}{x^2\sqrt{x^2+1}}>0\forall x\ne 0$.

BBT:

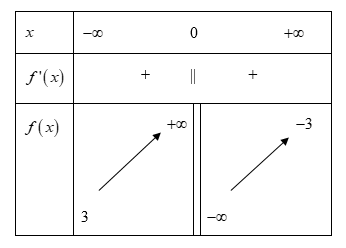
Dựa vào BBT ta thấy $\left(1\right)\iff m\ge -3,\left(2\right)\iff m\le 3\Rightarrow -3\le m\le 3.$

Mà $m\in \mathbb{Z}\Rightarrow m\in \left\{-3;-2;-1;0;1;2;3\right\}.$

Vậy có 7 giá trị nguyên của m thỏa mãn yêu cầu bài toán.

Chọn C.