Cho hình lăng trụ đứng ABC.A'B'C' có AB = AA' = 2a, AC = a, góc BAC = 120 độ

Phương pháp:

- Mặt cầu ngoại tiếp hình chóp ABCC'B' chính là mặt cầu ngoại tiếp lăng trụ đứng ABC.A'B'C'.

- Sử dụng công thức tính nhanh: Gọi R là bán kính mặt cầu ngoại tiếp lăng trụ, $R_{day}$ là bán kính đường tròn ngoại tiếp đáy ABC, ta có $R=\sqrt{\frac{h^2}{4}+R_{day}^2},$ với h là chiều cao hình trụ.

- Áp dụng định lí Cosin tính BC 

- Áp dụng định lí sin tính $R_{day}:\frac{BC}{\sin \angle BAC}=2R_{day}.$

Cách giải:

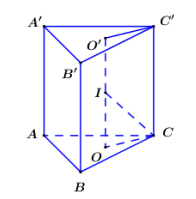
Mặt cầu ngoại tiếp hình chóp ABCC'B' chính là mặt cầu ngoại tiếp lăng trụ đứng ABC.A'B'C'

Gọi R là bán kính mặt cầu ngoại tiếp lăng trụ, $R_{day}$ là bán kính đường tròn ngoại tiếp đáy ABC, ta có $R=\sqrt{\frac{h^2}{4}+R_{day}^2}$, với h là chiều cao lăng trụ.

Ta có: $S_{\Delta ABC}=\frac{1}{2}.AB.AC.\sin \angle BAC=\frac{1}{2}.2a.a.\sin {120}^0=\frac{\sqrt{3}{a}^2}{2}.$

Áp dụng định lí Cosin trong tam giác ABC ta có $B{C}^2=A{B}^2+A{C}^2-2AB.AC.\cos \angle BAC=7a^2\Rightarrow BC=\sqrt{7}a.$

Áp dụng định lí Sin trong tam giác ABC ta có: $\frac{BC}{\sin \angle BAC}=2R_{day}\Rightarrow R_{day}=\frac{\sqrt{21}a}{3}.$

Vậy bán kính mặt cầu ngoại tiếp chóp ABCC'B' là: $R=\sqrt{\frac{h^2}{4}+R_{day}^2}=\sqrt{\frac{4a^2}{4}+\frac{7a^2}{3}}=\frac{\sqrt{30}a}{3}$

Chọn A.