Trong không gian Oxyz, cho mặt cầu (S): x^2 + (y - 2)^2 + (z +3)^2 = 24
Câu hỏi :
Trong không gian Oxyz, cho mặt cầu cắt mặt phẳng theo giao tuyến là đường tròn (C). Tìm hoành độ điểm M thuộc đường tròn (C) sao cho khoảng cách từ M đến A(6; -10; 3) lớn nhất.
A. -1
B. -4
C. 2
D. -5
A. 0
* Đáp án
B
* Hướng dẫn giải
Phương pháp:
- Xác định tâm I và bán kính R của mặt cầu (S).
- Gọi H là tâm đường tròn (C), tìm tọa độ điểm H. Gọi K là hình chiếu vuông góc của A lên tìm tọa độ điểm K.
- Sử dụng định lí Pytago: chứng minh
- Sử dụng BĐT tam giác: tìm M để
Cách giải:
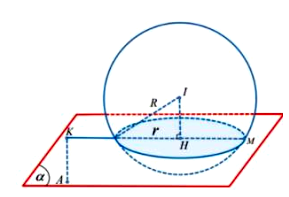
Mặt cầu có tâm I(0; 2; -3), bán kính
Gọi H là tâm đường tròn
Phương trình đường thẳng
Tọa độ điểm H là nghiệm của hệ phương trình
Ta có Bán kính đường tròn (C) là
Dễ thấy điểm A nằm ngoài mặt cầu (S). Gọi K là hình chiếu vuông góc của A lên tương tự như tìm tọa độ điểm H ta tìm được K(8; -8; 3).
Khi đó ta có
Áp dụng định lí Pytago ta có: do AK không đổi nên .
Ta cps (BĐT tam giác), do đó khi đó
Vậy
Chọn B.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Copyright © 2021 HOCTAP247
