Trang chủ
Đề thi & kiểm tra
Toán học
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Cho hai hàm số f(x) = a^3 + bx^2 +...
Cho hai hàm số f(x) = a^3 + bx^2 + cx - 1/2 và g(x) = dx^2 + ex + 1
Câu hỏi :
Cho hai hàm số và biết rằng đồ thị hàm số y = f(x) và y = g(x) cắt nhau tại 3 điểm có hoành độ lần lượt là -3; -1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng
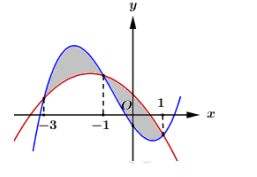
Cho hai hàm số và biết rằng đồ thị hàm số y = f(x) và y = g(x) cắt nhau tại 3 điểm có hoành độ lần lượt là -3; -1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng

A. 5
B.
C. 4
D. 8
* Đáp án
C
* Hướng dẫn giải
Phương pháp:
- Xét phương trình hoành độ, dựa vào số nghiệm của phương trình hoành độ giao điểm xác định chính xác f(x) - g(x)
- Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), y = g(x) đường thẳng x = a, x = b là
Cách giải:
Xét phương trình hoành độ giao điểm có 3 nghiệm lần lượt là -3; -1; 1 nên ta có
Nên
Hình phẳng giới hạn bởi hai đồ thị hàm số có diện tích bằng
= 2 - (-2) = 4.
Chọn C.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Số câu hỏi: 1500
Copyright © 2021 HOCTAP247
