Trang chủ
Đề thi & kiểm tra
Toán học
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Cho hàm số f(x) có đạo hàm liên tục trên...
Cho hàm số f(x) có đạo hàm liên tục trên R và có đồ thị hàm số f'(x) như hình vẽ
Câu hỏi :
Cho hàm số f(x) có đạo hàm liên tục trên và có đồ thị hàm số f'(x) như hình vẽ. Xét hàm số Mệnh đề nào dưới đây sai?
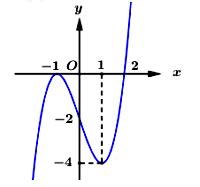
Cho hàm số f(x) có đạo hàm liên tục trên và có đồ thị hàm số f'(x) như hình vẽ. Xét hàm số Mệnh đề nào dưới đây sai?

A. Hàm số g(x) nghịch biến trên
B. Hàm số g(x) nghịch biến trên (0; 2)
C. Hàm số g(x) nghịch biến trên (-1; 0)
D. Hàm số g(x) đồng biến trên
* Đáp án
C
* Hướng dẫn giải
Phương pháp:
- Tính đạo hàm g'(x)
- Giải phương trình g'(x) = 0
- Lập BXD g'(x)
Cách giải:
Ta có
Khi đó (ta không xét và qua các nghiệm của phương trình này g'(x) không đổi dấu do x = -1 là nghiệm kép của phương trình f'(x) =0)
Lấy x = 3 ta có .
Bảng xét dấu g'(x)

Dựa vào bảng biến thiên ta thấy đáp án C sai.
Chọn C.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Số câu hỏi: 1500
Copyright © 2021 HOCTAP247
