Trong không gian Oxyz, cho ba điểm A(1; 1; 1), B(2; 1; 0), C(2; 0; 2)

* Hướng dẫn giải

Phương pháp:

- Gọi H, K lần lượt là hình chiếu vuông góc của A lên (P), BC Chứng minh $AH\le AK\Rightarrow d{\left(A;\left(P\right)\right)}_{\max }=AK.$

- Viết phương trình đường thẳng K tham số hóa tọa độ điểm $K\in BC.$

- Sử dụng $\overrightarrow{AK}.\overrightarrow{BC}=0$ tìm tọa độ vectơ $\overrightarrow{AK}.$

Cách giải:

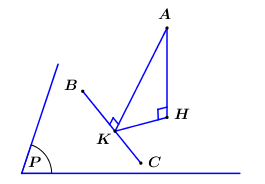
Gọi H, K lần lượt là hình chiếu vuông góc của A lên (P), BC.

Ta có $AH\perp \left(P\right)\Rightarrow AH\perp HK\Rightarrow \Delta AHK$ vuông tại $H\Rightarrow AH\le AK$ hay $d\left(A;\left(P\right)\right)\le d\left(A;BC\right)$.

Do đó d(A; (P)) lớn nhất khi $AH\equiv AK\Rightarrow H\equiv K.$

Ta có $\overrightarrow{BC}=\left(0;-1;2\right)\Rightarrow$ Phương trình đường thẳng $BC:\left\{\begin{array}{l}x=2\\ y=1-t\\ z=2t\end{array}\right.$

Vì $K\in BC\Rightarrow K\left(2;1-t;2t\right)\Rightarrow \overrightarrow{AK}=\left(1;-t;2t-1\right).$

Ta có $\overrightarrow{AK}.\overrightarrow{BC}=0\iff 1.0+t+2\left(2t-1\right)=0\iff t=\frac{2}{5}\Rightarrow \overrightarrow{AK}=\left(1;-\frac{2}{5};-\frac{1}{5}\right)//\left(5;-2;-1\right).$

Vậy khi d(A; (P)) lớn nhất thì (P) có 1 VTPT $\overrightarrow{n}=\left(5;-2;-1\right).$

Chọn D.