Trong không gian với hệ tọa độ Oxyz, cho điểm M thuộc mặt cầu

* Hướng dẫn giải

Phương pháp:

- Gọi M(x; y; z) tính $\overrightarrow{MA},\overrightarrow{MB},\overrightarrow{MC}$

- Từ giả thiết $M{A}^2+2\overrightarrow{MB}.\overrightarrow{MC}=8$ chứng minh $I\in \left(S\text{'}\right)$, xác định tâm I' và bán kính R' của mặt cầu (S').

- Xác định tâm I và bán kính R của mặt cầu (S).

- Chứng minh $II\text{'}<R+R\text{'}\Rightarrow \left(S\right)\cap \left(S\text{'}\right)=$ một đường tròn và M thuộc đường tròn đó.

- Sử dụng định lí Pytago tính bán kính của đường tròn.

Cách giải:

Gọi M(x; y; z) Ta có $\left\{\begin{array}{l}\overrightarrow{MA}=\left(1-x;-y;-z\right)\\ \overrightarrow{MB}=\left(2-x;1-y;3-z\right)\\ \overrightarrow{MC}=\left(-x;2-y;-3-z\right)\end{array}\right.$.

$\Rightarrow M{A}^2+2\overrightarrow{MB}.\overrightarrow{MC}=8$

$\iff {\left(1-x\right)}^2+y^2+z^2-2x\left(2-x\right)+2\left(1-y\right)\left(2-y\right)+2\left(3-z\right)\left(-3-z\right)=8$

$\iff x^2+y^2+z^2-2x+1-4x+2x^2+2\left(2-3y+y^2\right)-2\left(9-z^2\right)=8$

$\iff x^2+y^2+z^2-2x+1-4x+2x^2+4-6y+2y^2-18+2z^2=8$

$\iff 3x^3+3y^2+3z^2-6x-6y-21=0$

$\iff x^2+y^2+z^2-2x-7y-7=0\left(S\text{'}\right)$

$\Rightarrow M\in \left(S\text{'}\right)$ là mặt cầu tâm I'(1; 1; 0), bán kính $R\text{'}=\sqrt{1+1+7}=3.$

Hơn nữa, $M\in \left(S\right)$ có tâm I(3; 3; 2) bán kính R = 3

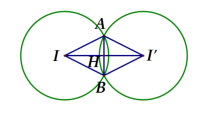
Ta có: $II\text{'}=\sqrt{2^2+2^2+2^2}=2\sqrt{3}<R+R\text{'}$.

$\Rightarrow M=\left(S\right)\cap \left(S\text{'}\right)$ là một đường tròn có bán kính r = AH

Dễ thấy $\Delta AII\text{'}$ cân tại A nên H là trung điểm của $II\text{'}\Rightarrow IH=\frac{1}{2}II\text{'}=\sqrt{3}.$

Vậy $r=AH=\sqrt{A{I}^2-I{H}^2}=\sqrt{3^2-{\left(\sqrt{3}\right)}^2}=\sqrt{6}$.

Chọn D.