Trong tất cả các khối chóp tứ giác đều ngoại tiếp mặt cầu bán kính bằng a

* Hướng dẫn giải

Phương pháp:

- Giả sử ta có khối chóp tứ giác đều S.ABCD. Xác định tâm mặt cầu nội tiếp khối chóp S.ABCD.

- Đặt SO = x > a tính SI, SH theo x, a.

- Sử dụng $\Delta SIH\backsim \Delta SMO\left(g.g\right),$ tính OM theo x, a từ đó tính $S_{ABCD}$ theo x, a.

- Tính $V_{S.ABCD}=\frac{1}{3}SO.S_{ABCD}$ theo x, a.

- Sử dụng phương pháp hàm số tìm GTNN của $V_{S.ABCD}$.

Cách giải:

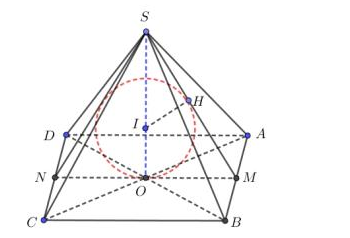
Giả sử ta có khối chóp tứ giác đều S.ABCD.

Gọi $O=AC\cap BD\Rightarrow SO\perp \left(ABCD\right)$.

Gọi M, N lần lượt là trung điểm của AB, AC Trong (SMN) dựng tia phân giác của góc $\angle SMN$ cắt SO tại $I\Rightarrow I$ là tâm mặt cầu nội tiếp khối chóp S.ABCD.

Kẻ $IH\perp SM\left(H\in SM\right)$ ta có r = IH = IO = a là bán kính mặt cầu nội tiếp khối chóp S.ABCD.

Đặt $SO=x>a\Rightarrow SI=SO-IO=x-a$

Áp dụng định lý Pytago ta có $SH=\sqrt{S{I}^2-I{H}^2}=\sqrt{{\left(x-a\right)}^2-a^2}=\sqrt{x^2-2ax}.$

Vì $\Delta SIH\backsim \Delta SMO\left(g.g\right)\Rightarrow \frac{SH}{SO}=\frac{IH}{OM}\Rightarrow \frac{\sqrt{x^2-2ax}}{x}=\frac{a}{OM}\Rightarrow OM=\frac{ax}{\sqrt{x^2-2ax}}$

$\Rightarrow AB=2OM=\frac{2ax}{\sqrt{x^2-2ax}}\Rightarrow S_{ABCD}=A{B}^2=\frac{4a^2{x}^2}{x^2-2ax}$

$\Rightarrow V_{S.ABCD}=\frac{1}{3}SO.S_{ABCD}=\frac{1}{3}x.\frac{4a^2{x}^2}{x^2-2ax}=\frac{4a^2}{3}.\frac{x^3}{x^2-2ax}.$

Xét hàm số $f\left(x\right)=\frac{x^3}{x^2-2ax}\left(x>0\right)$ ta có

$f\text{'}\left(x\right)=\frac{3x^2.\left(x^2-2ax\right)-x^3.\left(2x-2a\right)}{{\left(x^2-2ax\right)}^2}$

$f\text{'}\left(x\right)=\frac{3x^4-6a{x}^3-2x^4+2a{x}^3}{{\left(x^2-2ax\right)}^2}$

$f\text{'}\left(x\right)=\frac{x^4-4a{x}^3}{{\left(x^2-2ax\right)}^2}$

 

$f\text{'}\left(x\right)=0\iff x^3\left(x-4a\right)=0\iff x=4a\left(tm\right)$

$\Rightarrow \underset{\left(a;+\infty \right)}{\min }f\left(x\right)=f\left(4a\right)=\frac{64a^3}{{\left(4a\right)}^2-2a.4a}=8a.$

 

Vậy $\min V_{S.ABCD}=\frac{4a^2}{3}.8a=\frac{32a^3}{3}$, đạt được khi SO = 4a.

Chọn D.