Cho hình lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a và cạnh bên bằng . Lấy M, N lần lượt trên cạnh AB', A'C' sao cho . Tính thể tích V của khối .

Đáp án B

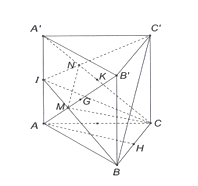
Gọi G, K lần lượt là tâm các hình chữ nhật $AB{B}^{\text{'}}{A}^{\text{'}}$  và $A{A}^{\text{'}}{C}^{\text{'}}C$  .

Ta có: $\frac{AM}{A{B}^{\text{'}}}=\frac{1}{3}\Rightarrow \frac{AM}{AG}=\frac{2}{3}$  (do G là trung điểm $A{B}^{\text{'}}$ ).

Xét tam giác $AB{A}^{\text{'}}$  có AG là trung tuyến và $\frac{AM}{AG}=\frac{2}{3}$ .

Suy ra M là trọng tâm tam giác $AB{A}^{\text{'}}$ .

Do đó BM đi qua trung điểm I của AA'  .

Ta có: $\frac{A^{\text{'}}N}{A^{\text{'}}C}=\frac{1}{3}\Rightarrow \frac{A^{\text{'}}N}{A^{\text{'}}K}=\frac{2}{3}$  (do K là trung điểm $A^{\text{'}}C$ ).

Xét tam giác AA'C   có A'K là trung tuyến và $\frac{A^{\text{'}}N}{A^{\text{'}}K}=\frac{2}{3}$  , suy ra N là trọng tâm của tam giác .

Do đó C'N đi qua trung điểm I của AA'  .

Từ M là trọng tâm tam giác ABA' và N trọng tâm của tam giác AA'C, suy ra: $\frac{IM}{IB}=\frac{IN}{I{C}^{\text{'}}}=\frac{1}{3}$  .

Gọi $V_1,{\text{ V}}_2$  lần lượt là thể tích các khối chóp IMNC; .

Ta có: $\frac{V_1}{V_2}=\frac{IM}{IB}.\frac{IN}{I{C}^{\text{'}}}.\frac{IC}{IC}=\frac{1}{9}$ .

Mà $V_1+V=V_2\Rightarrow V=\frac{8}{9}{V}_2$ .

Hạ AH vuông góc với BC tại H thuộc BC.

Ta được AH vuông góc với mặt phẳng ,  song song với mặt phẳng  nên khoảng cách từ I đến mặt phẳng  bằng khoảng cách từ A đến  và bằng AH.

Ta có: $AH=\frac{a\sqrt{3}}{2},{\text{ V}}_2=\frac{1}{3}d\left(I;\left(B{B}^{\text{'}}{C}^{\text{'}}C\right)\right).S_{\Delta BC{C}^{\text{'}}}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.\frac{a^2\sqrt{2}}{2}=\frac{a^3\sqrt{6}}{12}$ .

Suy ra:$V=\frac{8}{9}{V}_2=\frac{2{\text{a}}^3\sqrt{6}}{27}$ .