Trang chủ
Đề thi & kiểm tra
Toán học
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Cho tứ diện ABCD. Gọi M, N, P lần lượt...
Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC, AD
Câu hỏi :
Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC, AD và O là trọng tâm tam giác BCD. Tính tỉ số thể tích
Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC, AD và O là trọng tâm tam giác BCD. Tính tỉ số thể tích
A.
B.
C.
D.
* Đáp án
B
* Hướng dẫn giải
Phương pháp:
So sánh chiều cao và diện tích đáy của hai khối chóp.
Cách giải:
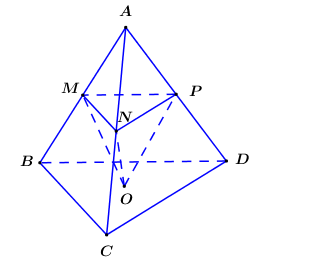
Vì theo tỉ số nên
Ta có
Lại có .
Vậy
Chọn B.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Số câu hỏi: 1500
Copyright © 2021 HOCTAP247
