Trang chủ
Đề thi & kiểm tra
Toán học
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Cho cấp số cộng (an) , cấp số nhân (bn)...
Cho cấp số cộng (an) , cấp số nhân (bn) thỏa mãn a2>a1>=0, b2>b1>=1 và hàm số f(x)=x^2-3x sao cho f(a1)+2=f(a1) và f(log2b1)+2=f(log2b1). Tìm số nguyên dương n nhỏ nhất sao cho bn>...
Câu hỏi :
Cho cấp số cộng , cấp số nhân thỏa mãn và hàm số sao cho và . Tìm số nguyên dương n nhỏ nhất sao cho .
A. 17.
B. 14.
C. 15.
D. 16.
* Đáp án
D
* Hướng dẫn giải
Đáp án D
Xét hàm số trên .
Ta có
Bảng biến thiên hàm số f(x) trên như sau:
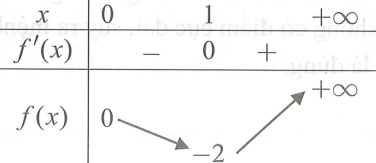
Vì nên
Giả sử , vì đồng biến trên nên suy ra vô lý.
Vậy do đó
Từ (1), (2) ta có:
Vậy số hạng tổng quát của dãy cấp số cộng là:
Đặt , suy ra: , vì nên , theo lập luận trên ta có:
Vậy số hạng tổng quát của dãy cấp số nhân là .
Do đó .
Trong 4 đáp án n=16 là số nguyên dương nhỏ nhất thỏa mãn (*).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Số câu hỏi: 1250
Copyright © 2021 HOCTAP247
