Trang chủ
Đề thi & kiểm tra
Toán học
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
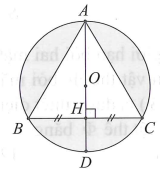
Cho đều cạnh a và nội tiếp trong đường tròn...
Cho đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần tô đậm quay quanh đường thẳng AD bằng:
Câu hỏi :
Cho đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần tô đậm quay quanh đường thằng AD bằng

A.
B.
C.
D.
* Đáp án
C
* Hướng dẫn giải
Đáp án C.
Gọi thể tích của khối tròn xoay sinh ra do phần tô đậm quay quanh đường thẳng AD là V1.
Gọi thể tích của khối tròn xoay sinh ra do hình tam giác ABC quay quanh đường thẳng AD là V2.
Gọi thể tích của khối tròn xoay sinh ra do hình tròn đường kính AD quay quanh đường thẳng AD là V3.
Khi đó:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Số câu hỏi: 1250
Copyright © 2021 HOCTAP247
