Trang chủ
Đề thi & kiểm tra
Toán học
25 đề thi thử Toán THPT Quốc gia có lời giải chi tiết !!
Xét tam giác ABC nhọn nội tiếp đường tròn (O;R).
Xét tam giác ABC nhọn nội tiếp đường tròn (O;R).
Câu hỏi :
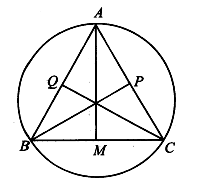
Xét tam giác ABC nhọn nội tiếp đường tròn(O;R) . Gọi lần lượt là thể tích của các khối tròn xoay sinh ra khi quay tam giác OCA quanh trung trực của đoạn thẳng CA, quay tam giác OAB quanh trung trực của đoạn thẳng AB, quay tam giac OBC quanh trung trực của đoạn thẳng BC. Khi biểu thức đạt giá trị lớn nhất, tính theo
A.
B.
C.
D.
* Đáp án
* Hướng dẫn giải
Xét hàm . Với .
Khi đó .
Lập bảng biến thiên, thấy rằng .
Khi đó, áp dụng cho : đạt giá trị lớn nhất khi .
Hay khi đó tam giác ABC cân tại A (do OP =OQ).
Mà lúc đó .
Do tam giác ABC cân A nên khi đó .
Ta có .
Mà .
Vậy
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
25 đề thi thử Toán THPT Quốc gia có lời giải chi tiết !!
Số câu hỏi: 1000
Copyright © 2021 HOCTAP247
