Cho f(x) là hàm số bậc ba thỏa mãn f(0) = 2 và f'(1) = 0. Hàm số
Câu hỏi :
Cho f(x) là hàm số bậc ba thỏa mãn f(0) = 2 và f'(1) = 0. Hàm số f'(x) có bảng biến thiên như sau:
* Đáp án
A
* Hướng dẫn giải
Chọn A.
Giả sử
Ta có
Dựa vào bảng biến thiên, ta suy ra đồ thị hàm số f'(x) đối xứng nhau qua trục tung nên là hàm chẵn suy ra b = 0.
Khi đó
Mặt khác cũng từ bảng biến thiến và giả thiết, ta có
Khi đó
Mà .
Vậy
Xét hàm số ta thấy h(x) là một hàm chẵn nên nhận trục tung là trục đối xứng, vì vậy số điểm cực trị của h(x) chính bằng hai lần số cực trị dương của hàm số công thêm 1.
Xét hàm số trên ta có
(do x > 0).
Bảng biến thiên
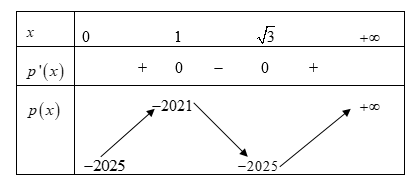
Từ bảng biến thiên, ta suy ra số điểm cực trị của hàm số h(x) là 2.2 + 1 = 5
Mặt khác, đồ thị của hàm số g(x) đối xứng qua Ox, do đó số điểm cực trị của hàm số g(x) bằng số điểm cực trị của hàm số h(x) cộng với số nghiệm bội lẻ của phương trình h(x) = 0.
Dựa vào bảng biến thiên ta có thấy h(x) = 0 có ha nghiệm bội đơn.
Vậy hàm số g(x) có tất cả 5 + 2 = 7 điểm cực trị.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Copyright © 2021 HOCTAP247
