Xét các số phức z, w thỏa mãn |z| = 2, |iw - 2 + 5i| = 1

* Hướng dẫn giải

Chọn D.

Gọi M(x; y) là điểm biểu diễn số phức $w=x+yi;x,y\in ℝ.$ Ta có

$\left|iw-2+5i\right|=1\iff \left|i\left(x+yi\right)-2+5i\right|=1\iff {\left(x+5\right)}^2+{\left(y+2\right)}^2=1.$

Tập hợp các điểm M là đường tròn tâm I(-5; -2) bán kính R = 1.

Ta có: $P=\left|z^2-wz-4\right|=\left|z^2-wz-{\left|z\right|}^2\right|=\left|z^2-wz-z.\overline{z}\right|=\left|z\right|\left|\left(z-\overline{z}\right)-w\right|=2\left|\left(z-\overline{z}\right)-w\right|.$

Đặt $z=a+bi;a,b\in ℝ,$ do $\left|z\right|=2\iff a^2+b^2=4\Rightarrow -2\le b\le 2.$

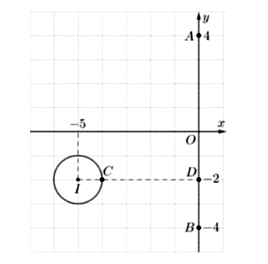
Gọi N là điểm biểu diễn số phức $z-\overline{z}=2bi\Rightarrow N\left(0;2b\right)$ nên N thuộc đoạn AB, với $A\left(0;4\right),B\left(0;-4\right).$ Khi đó $P=2\left|\left(z-\overline{z}\right)-w\right|=2MN\ge 2CD=8,$ dấu bằng xảy ra khi và chỉ khi $\left\{\begin{array}{l}M\equiv C\\ N\equiv D\end{array}\right..$

Vậy giá trị nhỏ nhất của $\left|z^2-wz-4\right|$ bằng 8.