Trang chủ
Đề thi & kiểm tra
Toán học
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Cho khối chóp S.ABCD có đáy là hình bình hành,...
Cho khối chóp S.ABCD có đáy là hình bình hành, có thể tích bằng
Câu hỏi :
Cho khối chóp S.ABCD có đáy là hình bình hành, có thể tích bằng Gọi E là trung điểm SC. Một mặt phẳng chứa AE cắt các cạnh SB và SD lần lượt tại M và N. Tìm giá trị nhỏ nhất của thể tích khối chóp S.AMEN.
A.
B.
C.
D.
* Đáp án
A
* Hướng dẫn giải
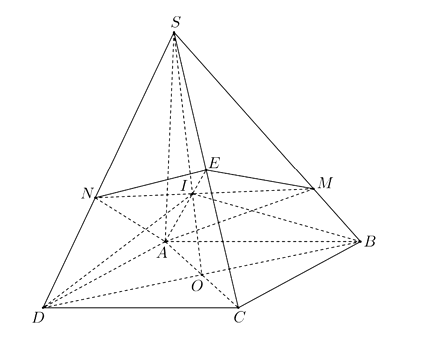
Mặt đáy ABCD là hình bình hành và có cùng diện tích
(hai khối chóp có cùng chiều cao và có diện tích mặt đáy bằng nhau).
Mà
Gọi O là giao điểm của AC và BD; I là giao điểm của SO và là trọng tâm của và I thuộc MN. Gọi và
Ta có: và
và và
Do đó:
Mặt khác: và có chung chiều cao kẻ từ I và có đáy
Mà I là trọng tâm của
Chứng minh tương tự ta có:
O là trung điểm của hay
Theo bất đẳng thức AM-GM, ta có:
(do hay
Dấu “=” xảy ra khi và chỉ khi đi qua I và MN//BD.
Vậy giá trị nhỏ nhất của thể tích khối chóp S.AMEN là
Chọn A.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Số câu hỏi: 1500
Copyright © 2021 HOCTAP247
