Trang chủ
Đề thi & kiểm tra
Toán học
25 đề thi thử Toán THPT Quốc gia có lời giải chi tiết !!
Cho hình chóp S.ABC có SA=SB=SC= a
Cho hình chóp S.ABC có SA=SB=SC= a
Câu hỏi :
Cho hình chóp S.ABC có , , và . Tính khoảng cách d giữa hai đường thẳng AC và SB.
Cho hình chóp S.ABC có , , và . Tính khoảng cách d giữa hai đường thẳng AC và SB.
A.
B.
C.
D.
* Đáp án
C
* Hướng dẫn giải
Đáp án C
Ta thấy vuông tại B.
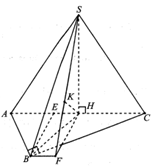
Khi đó gọi H là trung điểm AC, do nên .
Gọi E là hình chiếu vuông góc của B xuống AC.
Trên đường thẳng d qua B và song song với AC lấy điểm F sao cho ta có .
Kẻ .
Ta có: .
Vậy .
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
25 đề thi thử Toán THPT Quốc gia có lời giải chi tiết !!
Số câu hỏi: 1000
Copyright © 2021 HOCTAP247
