Trang chủ
Đề thi & kiểm tra
Toán học
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
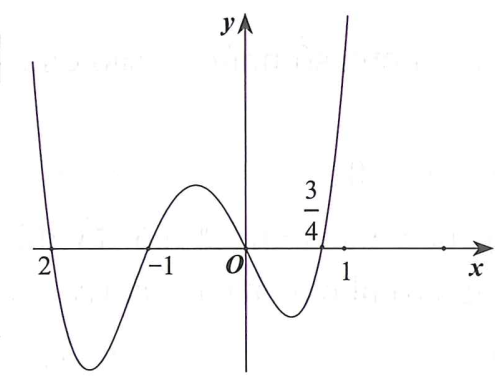
Cho hàm số bậc bốn y=f(x) có đồ thị như...
Cho hàm số bậc bốn y=f(x) có đồ thị như hình vẽ dưới đây.
Câu hỏi :
Cho hàm số bậc bốn y=f(x) có đồ thị như hình vẽ dưới đây.
Số điểm cực trị của hàm số là
Cho hàm số bậc bốn y=f(x) có đồ thị như hình vẽ dưới đây.

Số điểm cực trị của hàm số là
A. 5.
B. 3.
C. 7.
D. 11.
* Đáp án
C
* Hướng dẫn giải
Đáp án C.
Do là hàm số bậc bốn nên là hàm số liên tục và có đạo hàm luôn xác định với mọi x.
Theo đồ thị hàm số ta có được
Mặt khác
Xét hàm số trên
Ta có từ đó ta có bảng biến thiên của như sau:
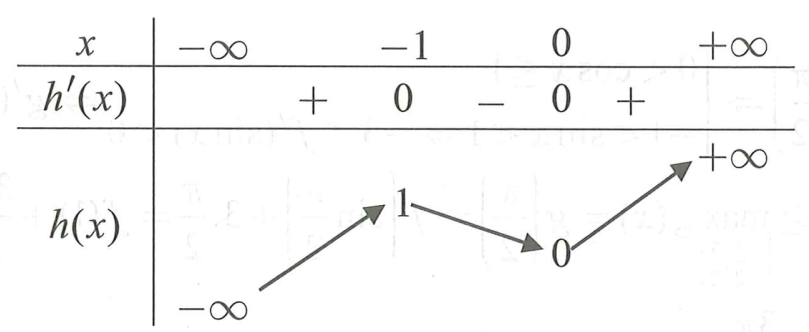
Từ BBT của hàm số nên ta có có đúng một nghiệm, có đúng 1 nghiệm, có đúng ba nghiệm phân biệt và các nghiệm này đều khác 0 và
Vì thế phương trình có đúng bảy nghiệm phân biệt và đều là các nghiệm đơn nên hàm số có 7 cực trị.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Số câu hỏi: 1250
Copyright © 2021 HOCTAP247
