Trong không gian Oxyz, cho điểm A(0; 4; -3). Xét mặt phẳng (P) thay đổi

Chọn A.

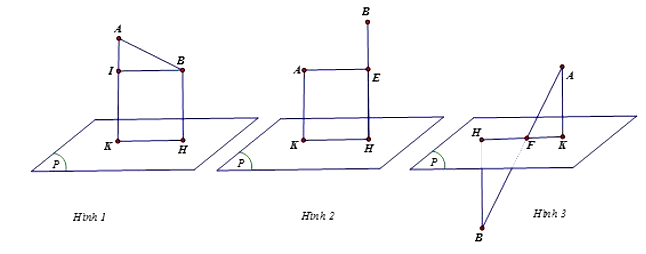
Ta có $\overrightarrow{AB}\left(4;-4;2\right)\Rightarrow AB=\sqrt{4^2+{\left(-4\right)}^2+2^2}=6.$

Trường hợp 1: Hai điểm A, B nằm cùng phía so với (P) có hai hình vẽ biểu diễn là hình 1 và hình 2.

Từ hình vẽ 1 ta có $d\left(A,\left(P\right)\right)=AK,d\left(B;\left(P\right)\right)=BH=3.$

$AK=AI+IK\le AB+BH=6+3=9$ (do $IK=BH,AI\le AB$).

Suy ra AK lớn nhất bằng 9 khi AI = AB điều này xảy ra khi A, B, H thẳng hàng và H = K.

Vậy d(A, (P)) lớn nhất bằng 9 và (P) nhận $\overrightarrow{AB}\left(4;-4;2\right)$ làm véc tơ pháp tuyến.

Mặt phẳng (P) nhận $\overrightarrow{n}\left(2;-2;1\right)$ là véc tơ pháp tuyến có phương trình dạng $2x-2y+z+D=0.$

$d\left(A,\left(P\right)\right)=9\iff \frac{\left|D-11\right|}{3}=9\iff \left[\begin{array}{l}D=38\\ D=-16\end{array}\right..$

Vậy (P) có phương trình $2x-2y+z+38=0$ và $2x-2y+z-16=0.$

Đối chiếu các phương án ta thấy có phương án A thỏa mãn.

Từ hình vẽ ta có $d\left(A,\left(P\right)\right)=AH=EH<BK=3<9$ nên loại.

Trường hợp 2: Hai điểm A, B nằm khác phía so với (P).

Từ hình vẽ 3 ta có $d\left(A,\left(P\right)\right)=AK<AF<AB=6<9$ nên loại.

Vậy đáp án là phương án A.