Cho đồ thị hàm số y = f'(x) như hình vẽ, biết f''(3) = 2/3. Hỏi có tất cả
Câu hỏi :
Cho đồ thị hàm số y = f'(x) như hình vẽ, biết Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số có đúng bốn điểm cực trị?
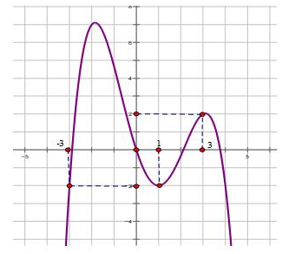
Cho đồ thị hàm số y = f'(x) như hình vẽ, biết Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số có đúng bốn điểm cực trị?

* Đáp án
D
* Hướng dẫn giải
Chọn D.
Xét hàm số
Ta có:
Đặt suy ra (*) có dạng:
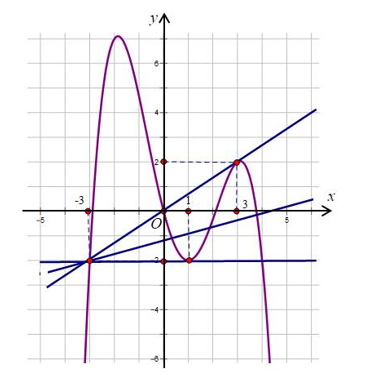
Số nghiệm bội lẻ của phương trình g'(x) = 0 bằng với số nghiệm bội lẻ của phương trình tương đương với số giao điểm không tiếp xúc của hai đồ thị y = f'(t) và đường thẳng
Đường thẳng d luôn đi qua A(-3; -2)
Gọi là đường thẳng đi qua A và tiếp xúc với đồ thị hàm số y = f'(t) tại điểm (3; 2) như hình vẽ.
Suy ra: khi đó giá trị tham số thỏa mãn
Gọi là đường thẳng đi qua A và tiếp xúc với đồ thị hàm số y = f'(t) tại điểm (1; -2) như hình vẽ.
Suy ra: khi đó giá trị tham số thỏa mãn
Để hàm số g(x) có bốn điểm cực trị thì phương trình có bốn nghiệm bội lẻ, tương đương với đồ thị y = f'(t) và đường thẳng d có bốn giao điểm xuyên qua.
Do đó
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Copyright © 2021 HOCTAP247
