Trang chủ
Đề thi & kiểm tra
Toán học
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Người ta sản xuất một vật lưu niệm (N) bằng...
Người ta sản xuất một vật lưu niệm (N) bằng thủy tinh trong suốt có dạng khối tròn xoay mà thiết kế qua trục của nó là một hình thang cân (xem hình vẽ). Bên trong (N) có hai khối c...
Câu hỏi :
Người ta sản xuất một vật lưu niệm (N) bằng thủy tinh trong suốt có dạng khối tròn xoay mà thiết kế qua trục của nó là một hình thang cân (xem hình vẽ). Bên trong (N) có hai khối cầu ngũ sắc với bán kính lần lượt là , tiếp xúc với nhau và cùng tiếp xúc với mặt xung quanh của (N), đồng thời hai khối cầu lần lượt tiếp xúc với hai mặt đáy của (N). Tính thể tích của vật lưu niệm đó
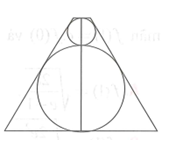
Người ta sản xuất một vật lưu niệm (N) bằng thủy tinh trong suốt có dạng khối tròn xoay mà thiết kế qua trục của nó là một hình thang cân (xem hình vẽ). Bên trong (N) có hai khối cầu ngũ sắc với bán kính lần lượt là , tiếp xúc với nhau và cùng tiếp xúc với mặt xung quanh của (N), đồng thời hai khối cầu lần lượt tiếp xúc với hai mặt đáy của (N). Tính thể tích của vật lưu niệm đó

A. .
B. .
C. .
D. .
* Đáp án
D
* Hướng dẫn giải
Đáp án D
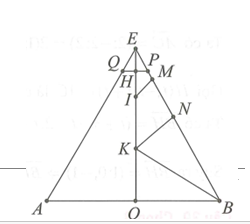
Giả sử thiết diện là hình thang ABPQ
Gọi I, K lần lượt là tâm của đường tròn nhỏ và to.
Gọi M, N là hình chiếu của I, K lên một cạnh bên, điểm (hình vẽ) trong đó .
Ta có:
Suy ra
Mặt khác ,
Thể tích của vật thể cần tìm là:Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Số câu hỏi: 1250
Copyright © 2021 HOCTAP247
