Trang chủ
Đề thi & kiểm tra
Toán học
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Cho hàm số f(x) liên tục trên có f(0)=0 và...
Cho hàm số f(x) liên tục trên có f(0)=0 và đồ thị hàm số y=f'(x) như hình vẽ bên. Hàm số y=|3f(x)-x^3| đồng biến trên khoảng
Câu hỏi :
Cho hàm số f(x) liên tục trên có f(0)=0 và đồ thị hàm số y=f'(x) như hình vẽ bên. Hàm số đồng biến trên khoảng
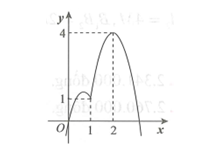

A. .
B. .
C. .
D. .
* Đáp án
C
* Hướng dẫn giải
Đáp án C
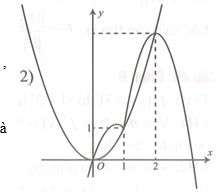
Xét hàm số
Vẽ đồ thị hàm số ta thấy , ,
Do đó hàm số đồng biến trên khoảng (0;2) và
Do đó , đồng biến trên khoảng .
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Số câu hỏi: 1250
Copyright © 2021 HOCTAP247
