Trang chủ
Đề thi & kiểm tra
Toán học
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Một biển quảng cáo có dạng hình Elip với bốn...
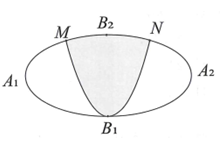
Một biển quảng cáo có dạng hình Elip với bốn đỉnh A1 , A2, A3, như hình vẽ bên. Người ta chia Elip bởi Parabol có đỉnh B1, trục đối xứng B1B2, và đi qua các điểm M, N
Câu hỏi :
Một biển quảng cáo có dạng hình Elip với bốn đỉnh A1 , A2, A3, như hình vẽ bên. Người ta chia Elip bởi Parabol có đỉnh B1, trục đối xứng B1B2, và đi qua các điểm M, N. Sau đó sơn phần tô đậm với giá 200.000 đồng/ và trang trí đèn Led phần còn lại với giá 500.000 đồng/ . Hỏi kinh phí sử dụng gần nhất với giá trị nào dưới đây? Biết rằng , , .

A. 2.341.000 đồng.
B. 2.057.000 đồng.
C. 2.760.000 đồng.
D. 1.664.000 đồng.
* Đáp án
A
* Hướng dẫn giải
Đáp án A
Chọn hệ tọa độ Oxy, với O là trung điểm ,
Phương trình mà , thuộc ,
Gọi phương trình parabol (P) là
Dựa vào hình vẽ, ta thấy (P) có đỉnh và đi qua
Khi đó, diện tích phần tô đậm là .
Diện tích của elip là Diện tích phần còn lại là
Vậy kinh phí sử dụng để trang trí là đồngCâu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Số câu hỏi: 1250
Copyright © 2021 HOCTAP247
