Trang chủ
Đề thi & kiểm tra
Toán học
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Cho hàm số y = f(x) là hàm đa thức...
Cho hàm số y = f(x) là hàm đa thức bậc bốn. Đồ thị hàm y = f'(x - 1) được
Câu hỏi :
Cho hàm số y = f(x) là hàm đa thức bậc bốn. Đồ thị hàm y = f'(x - 1) được cho trong hình vẽ bên. Hàm số đồng biến trên khoảng nào sau đây?
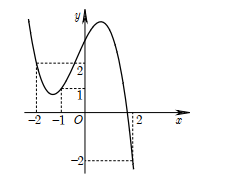

A. (-2; -1)
B. (1; 2)
C. (0; 1)
D. (-1; 0)
* Đáp án
D
* Hướng dẫn giải
Ta có:
Cho
Đặt 2x = X - 1 ta có khi đó số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f'(X - 1) và Y = -X
Ta có đồ thị hàm số:
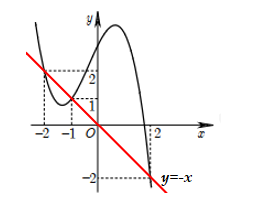
Dựa vào đồ thị qua các nghiệm này g'(x) đổi dấu.
Ta có (do ) nên ta có BXD g'(x) như sau:
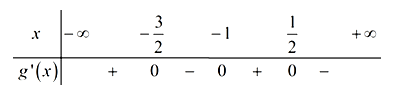
Vậy hàm số đồng biến trên khoảng (-1; 0).
Chọn D.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Số câu hỏi: 1500
Copyright © 2021 HOCTAP247
