Cho số phức z thỏa mãn |z-4+z ngang|+|z+z ngang|>=4 và số phức w=(x-2i)(z ngang.i +2-4i) có phần ảo là số thực không dương. Trong mặt phẳng tọa độ Oxy, hình phẳng (H) là tập hợp cá...

Đáp án C         

Gọi $M\left(x;y\right)$  là điểm biểu diễn của số phức $z=x+iy\left(x^2+y^2>0\right)$

Ta có: $\left|z-4+\overline{z}\right|+\left|z-\overline{z}\right|\ge 4\iff \left|2\text{x}-4\right|+\left|2y\right|\ge 4\iff \left|x-2\right|+\left|y\right|\ge 2$

* $\text{w}=\left(z-2i\right)\left(\overline{z}i+2-4i\right)=\left(x+\left(y-2\right)i\right)\left(\left(x-yi\right)i+2-4i\right)$

$\left(x+\left(y-2\right)i\right)\left(y+2+\left(x-4\right)i\right)=x\left(y+2\right)-\left(x-4\right)\left(y-2\right)+\left[x\left(x-4\right)+y^2-4\right]i$Theo giả thiết, ta có: $x\left(x-4\right)+y^2-4\le 0\iff x^2+y^2-4\text{x}-4\le 0$

Vậy tập hợp điểm biểu diễn của số phức z thỏa mãn: 

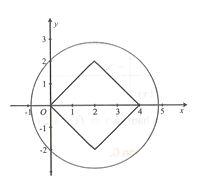
$\left\{\begin{array}{l}\left|x-2\right|+\left|y\right|\ge 2\\ x^2+y^2-4\text{x}-4\le 0\end{array}\right.$ có miền là hình vẽ dưới đây:

Hình phẳng  là phần không gian nằm bên ngoài hình vuông cạnh bằng 2 và nằm bên trong hình tròn (C) có tâm $I\left(2;0\right)$  và bán kính $R=\sqrt{4+4}=2\sqrt{2}$ .

Diện tích hình (H) là $S=\pi R^2-2^2=\pi {\left(2\sqrt{2}\right)}^2-4=8\pi -4\simeq \mathrm{21,13}$ .