Trang chủ
Đề thi & kiểm tra
Toán học
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Tìm các giá trị của tham số m để đồ...
Tìm các giá trị của tham số m để đồ thị hàm số y=x^4-2m^2x^2+m^4+1 có ba điểm cực trị. Đồng thời ba điểm cực trị đó cùng với gốc O tạo thành một tứ giác nội tiếp.
Câu hỏi :
Tìm các giá trị của tham số m để đồ thị hàm số có ba điểm cực trị. Đồng thời ba điểm cực trị đó cùng với gốc O tạo thành một tứ giác nội tiếp.
A.
B.
C.
D. Không tồn tại m.
* Đáp án
A
* Hướng dẫn giải
Đáp án A
|
Ta có
Điều kiện để hàm số có 3 điểm cực trị là
Gọi là các điểm cực trị của đồ thị hàm số đã cho. Vì B, C đối xứng nhau qua trục Oy và nên Lại có cạnh OA chung nên (c-c-c) suy ra |
|
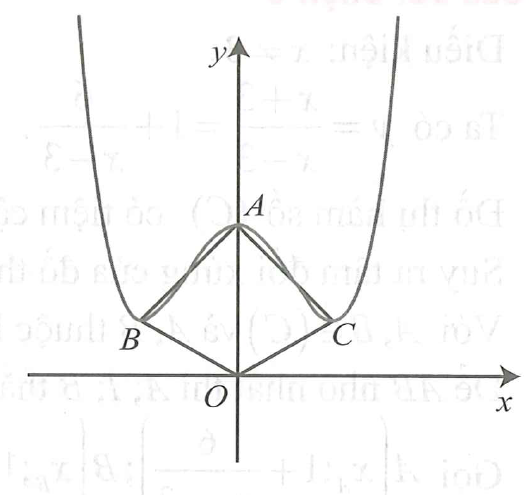
mà tứ giác OBAC nội tiếp nên
Hay
Ta có
Vậy
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Số câu hỏi: 1250
Copyright © 2021 HOCTAP247
