Trang chủ Đề thi & kiểm tra Toán học Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !! Bác Bính có một tấm thép mỏng hình tròn tâm...

Bác Bính có một tấm thép mỏng hình tròn tâm bán kính . Bác định cắt ra một hình quạt tròn tâm , quấn rồi hàn ghép hai mép của hình quạt tròn lại để tạo thành một đồ vật dạng mặt nó...

Câu hỏi :

Bác Bính có một tấm thép mỏng hình tròn tâm O bán kính 4dm. Bác định cắt ra một hình quạt tròn tâm O, quấn rồi hàn ghép hai mép của hình quạt tròn lại để tạo thành một đồ vật dạng mặt nón tròn xoay (tham khảo hình vẽ). Dung tích lớn nhất có thể của đồ vật mà bác Bính tạo ra bằng bao nhiêu? (Bỏ qua phần mối hàn và độ dày của tấm thép)
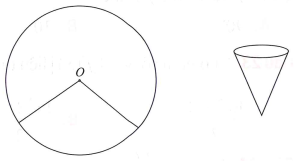
Bác Bính có một tấm thép mỏng hình tròn tâm bán kính . Bác định cắt ra một hình quạt tròn tâm , quấn rồi hàn ghép hai mép của hình quạt tròn lại để tạo thành một đồ vật dạng mặt nón tròn xoay (tham khảo hình vẽ). Dung tích lớn nhất có thể của đồ vật mà bác Bính tạo ra bằng bao nhiêu? (Bỏ qua phần mối hàn và độ dày của tấm thép) (ảnh 1)

A. 128π381dm3 .

B. 16π327dm3 .

C. 64π327dm3 .

D. 128π327dm3 .

* Đáp án

D

* Hướng dẫn giải

Đáp án D

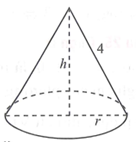
Bác Bính có một tấm thép mỏng hình tròn tâm bán kính . Bác định cắt ra một hình quạt tròn tâm , quấn rồi hàn ghép hai mép của hình quạt tròn lại để tạo thành một đồ vật dạng mặt nón tròn xoay (tham khảo hình vẽ). Dung tích lớn nhất có thể của đồ vật mà bác Bính tạo ra bằng bao nhiêu? (Bỏ qua phần mối hàn và độ dày của tấm thép) (ảnh 2)

Gọi bán kính đáy hình nón là r.

Ta có: Vn=13πr2h=13πr216−r2  với 0<r<4 .

Xét hàm f(r)=r216−r2  trên (0;4)  có:

f'(r)=2r16−r2+r.−r16−r2=32−3r316−r2=0⇔[r=463∈(0;4)r=−463∉(0;4)r=0∉(0;4)

Bảng biến thiên:

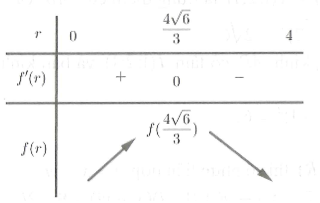
Bác Bính có một tấm thép mỏng hình tròn tâm bán kính . Bác định cắt ra một hình quạt tròn tâm , quấn rồi hàn ghép hai mép của hình quạt tròn lại để tạo thành một đồ vật dạng mặt nón tròn xoay (tham khảo hình vẽ). Dung tích lớn nhất có thể của đồ vật mà bác Bính tạo ra bằng bao nhiêu? (Bỏ qua phần mối hàn và độ dày của tấm thép) (ảnh 3)

Từ bảng biến thiên ta thấy, hàm số f(r) đạt GTLN khi .r=463

Vậy Vmax=13π(463)2⋅16−(463)2=128π327(dm3) .

Câu hỏi trên thuộc đề trắc nghiệm dưới đây !

Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!

Số câu hỏi: 1250

Toán học

Home
Tiểu học Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Hóa học Tài liệu Đề thi & kiểm tra Câu hỏi hoctapsgk.com Nghe truyện audio Đọc truyện chữ Công thức nấu ăn

Copyright © 2021 HOCTAP247