Trang chủ
Đề thi & kiểm tra
Toán học
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Cho phương trình: e^2m+e^m=2(x+căn (1-x^2)(1+x căn 1-x^2) . Tìm tất...
Cho phương trình: e^2m+e^m=2(x+căn (1-x^2)(1+x căn 1-x^2) . Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm.
Câu hỏi :
Cho phương trình: . Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm.
Cho phương trình: . Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm.
A.
B.
C.
D.
* Đáp án
B
* Hướng dẫn giải
Đáp án B
Điều kiện: .
Đặt .
Ta có: .
Bảng biến thiên:
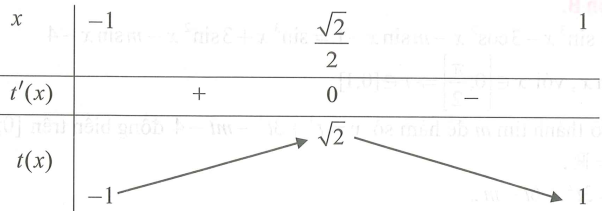
Từ bảng biến thiên ta có: .
Khi đó phương trình trở thành: .
Xét hàm số ta có Hàm số đồng biến trên Hàm số đồng biến trên
Từ
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Số câu hỏi: 1250
Copyright © 2021 HOCTAP247
