Cho hình chóp S.ABCD có SA vuông góc với đáy; SA=a căn 6. Đáy ABCD là hình thang vuông tại A và B, AB=BC=1/2AD=a. Gọi E là trung điểm AD. Tính bán kính mặt cầu ngoại tiếp hình chóp...

Đáp án B

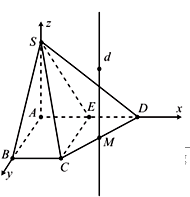
Vì E là trung điểm AD và $AB=BC=\frac{1}{2}A\text{D}=a$  nên $AB=BC=A\text{E}=E\text{D}=a$  mà $BC\text{ // AE}\Rightarrow$  tứ giác ABCE là hình vuông suy ra  hay tam giác ECD vuông tại E nên M là tâm đường tròn ngoại tiếp $\Delta EC\text{D}$ .

Gắn với hệ trục tọa độ với $A\equiv O(0;0;0),A\text{D}\equiv \text{Ox; AB}\equiv \text{Oy; AS}\equiv \text{Oz}$ .

Coi đơn vị độ dài là a=1

Suy ra $A(0;0;0),\text{ S}(0;0;\sqrt{6}),\text{ E}(1;0;0),\text{ D}(2;0;0),\text{ C}(1;1;0)$  và $M(\frac{3}{2};\frac{1}{2};0)$  là trung điểm của CD.

Vì  vuông tại E nên tâm mặt cầu ngoại tiếp hình chóp S.ECD thuộc đường thẳng qua M và song song với SA.

Phương trình đường thẳng d qua M và song song với SA có 1 véctơ pháp tuyến thì có dạng:  $d:\{\begin{array}{l}x=\frac{3}{2}\\ y=\frac{1}{2}\\ z=t\end{array}$  

Suy ra $I(\frac{3}{2};\frac{1}{2};t)$  là tâm mặt cầu ngoại tiếp chóp S.ECD thì:

$\text{IS}=I\text{D}\iff {\left(\frac{3}{2}\right)}^2+{\left(\frac{1}{2}\right)}^2+{(t-\sqrt{6})}^2={(-\frac{1}{2})}^2+{\left(\frac{1}{2}\right)}^2+t^2$

$\iff 2\sqrt{6}t=8\Rightarrow t=\frac{4}{\sqrt{6}}\Rightarrow I(\frac{3}{2};\frac{1}{2};\frac{4}{\sqrt{6}})$

Bán kính mặt cầu là $R=I\text{D}=\sqrt{{(-\frac{1}{2})}^2+{\left(\frac{1}{2}\right)}^2+{\left(\frac{4}{\sqrt{6}}\right)}^2}=\sqrt{\frac{19}{6}}$  hay $R=\sqrt{\frac{19}{6}}a$ .