Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với

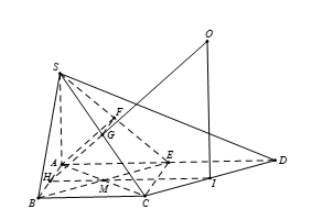
Gọi H, G, F lần lượt là trung điểm của AB, SC, SE và $M=AC\cap BD.$

Dễ thấy AFGH là hình bình hành.

Ta có $\left\{\begin{array}{l}AF\perp SE\left(SA=AE\right)\\ GF\perp SE\left(GF//AB//CE,AB\perp SE\right)\end{array}\right.\Rightarrow SE\perp \left(AFGH\right).$

Khi đó (AFGH) là mặt phẳng trung trực của SE.

Theo bài ra ta có: ABCE là hình vuông $\Rightarrow CE\perp AD\Rightarrow \Delta CED$ vuông tại E

Gọi I là trung điểm của $CD\Rightarrow I$ là tâm đường tròn ngoại tiếp tam giác CDE.

Qua I kẻ đường thẳng $d//SA\Rightarrow d$ là trục đường tròn ngoại tiếp tam giác CDE.

Ta gọi $O=GH\cap d\Rightarrow O$ là tâm mặt cầu ngoại tiếp hình chóp S.CDE, bán kính R = OC.

Ta có $IC=\frac{1}{2}CD=\frac{\sqrt{2}}{2}.$

$\Delta OIH\backsim \Delta GMH\Rightarrow \frac{GM}{MH}=\frac{OI}{IH}\Rightarrow OI=\frac{3}{2}.$

Áp dụng định lí Pytago trong tam giác OIC ta có $\Delta OIH\backsim \Delta GMH\Rightarrow \frac{GM}{MH}=\frac{OI}{IH}\Rightarrow OI=\frac{3}{2}.$

Vậy diện tích mặt cầu ngoại tiếp hình chóp S.CED là: $S_{mc}=4\pi R^2=4\pi .{\left(\frac{\sqrt{11}}{2}\right)}^2=11\pi .$

Chọn B.