Trang chủ
Đề thi & kiểm tra
Toán học
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Cho hình vuông OABC có cạnh bằng 4 được chia...
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay...
Câu hỏi :
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox.
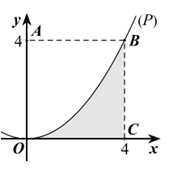
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox.

A.
B.
C.
D.
* Đáp án
D
* Hướng dẫn giải
Đáp án D
Phương trình parabol (P) có dạng đi qua điểm .
nên .
Gọi (H) là phần diện tích hình phẳng giới hạn bởi đường thẳng y=4, đồ thị hàm số và đường thẳng x=0.
Khi đó, thể tích khối tròn xoay tạo thành khi quay (H) quanh Ox là:
.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Số câu hỏi: 1250
Copyright © 2021 HOCTAP247
