Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân có AB=BC=a . Cạnh bên SA vuông góc với đáy, góc SBA=60 độ . Gọi M là điểm nằm trên AC sao cho AC=2CM . Tính khoảng cách giữa SM...

Đáp án D

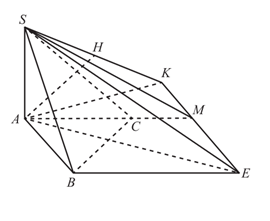
Trong (ABC), qua M kẻ đường thẳng song song với AB, qua B kẻ đường thẳng song song với AM. Hai đường thẳng này cắt nhau tại E ta được tứ giác ABEM là hình bình hành.

Vì $\begin{array}{l}ME//AB\Rightarrow AB//\left(SME\right)\\ \Rightarrow d(AB;SM)=d(AB;\left(SME\right))=d(A;\left(SME\right))\end{array}$

Từ A trong mặt phẳng (ABEM)   kẻ $AK\perp ME$ , lại có:  (do ).

Trong $\left(SAK\right)$   kẻ $AH\perp SK$  tại H.

Ta có  (do $SA\perp \left(ABEM\right)\Rightarrow EK\perp \left(SAK\right)$ )

 $\Rightarrow AH\perp \left(SKE\right)$  tại H.

Từ đó $d(AB;SM)=d(A;\left(SME\right))=AH$ .

Xét tam giác SBA vuông tại A có $SA=AB.\tan SBA=a.\tan 60°=a\sqrt{3}$ .

Lại có tam giác ABC vuông cân tại B nên $AC=AB\sqrt{2}=a\sqrt{2}\Rightarrow CM=\frac{AC}{2}=\frac{a\sqrt{2}}{2}$ .

Do đó $AM=AC+CM=\frac{3a\sqrt{2}}{2}$ .

 $\Delta ABC$vuông cân tại B nên $ACB=45°\Rightarrow CBE=ACB=45°$  (hai góc so le trong). 

Từ đó $ABE=ABC=CBE=90°+45°=135°$ , suy ra  (hai góc đổi hình bình hành).

Nên tam giác AME là tam giác tù nên K nằm ngoài đoạn ME.

Ta có:  mà tam giác AMK vuông tại K nên tam giác AMK vuông cân tại K. $\Rightarrow AK=\frac{AM}{\sqrt{2}}=\frac{3a}{2}$

Xét tam giác SAK vuông tại A có đường cao AH, ta có: $\frac{1}{A{H}^2}=\frac{1}{S{A}^2}+\frac{1}{A{K}^2}=\frac{1}{3a^2}+\frac{1}{9a^2}\Rightarrow AH=\frac{3a\sqrt{7}}{7}$ .

Vậy $d(AB;SM)=\frac{3a\sqrt{7}}{7}$